Verification of Binarized Neural Networks via Inter-Neuron Factoring
Paper and Code
Jan 19, 2018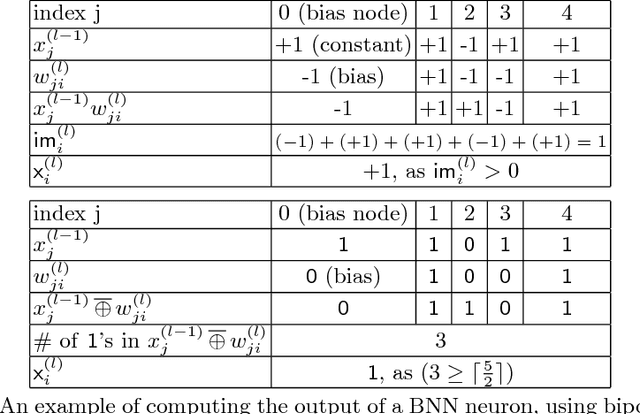
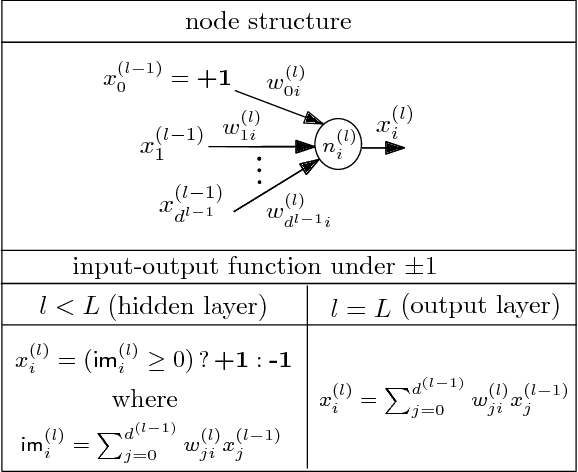
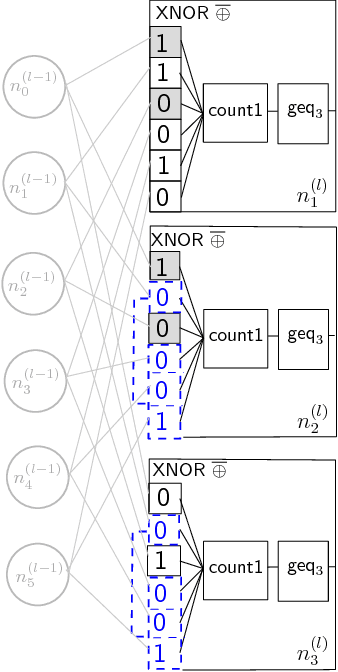
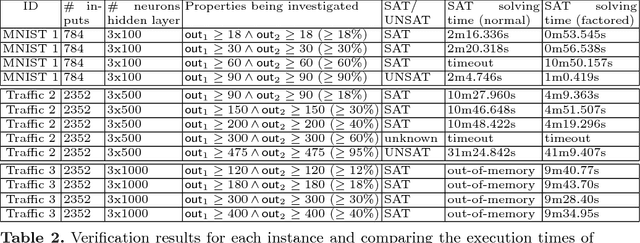
We study the problem of formal verification of Binarized Neural Networks (BNN), which have recently been proposed as a energy-efficient alternative to traditional learning networks. The verification of BNNs, using the reduction to hardware verification, can be even more scalable by factoring computations among neurons within the same layer. By proving the NP-hardness of finding optimal factoring as well as the hardness of PTAS approximability, we design polynomial-time search heuristics to generate factoring solutions. The overall framework allows applying verification techniques to moderately-sized BNNs for embedded devices with thousands of neurons and inputs.
* Version 2: add proofs for hardness of PTAS approximability, remove
experiments on randomized examples and some not-so-important optimizations
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge