Variable Metric Proximal Gradient Method with Diagonal Barzilai-Borwein Stepsize
Paper and Code
Oct 15, 2019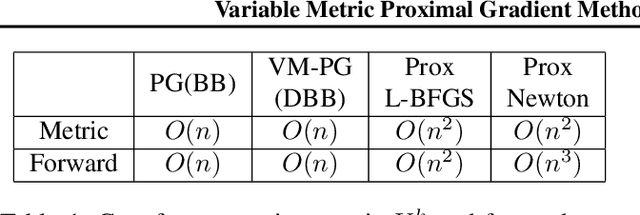
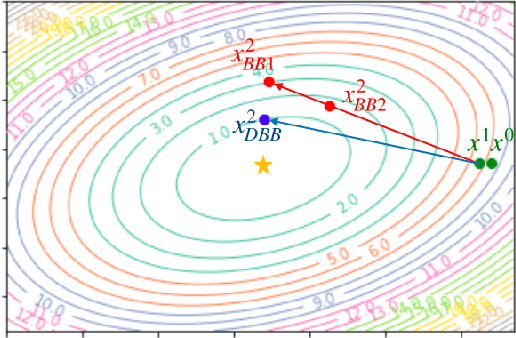

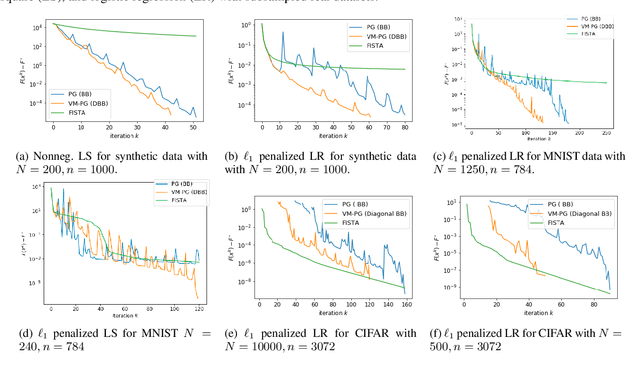
Variable metric proximal gradient (VM-PG) is a widely used class of convex optimization method. Lately, there has been a lot of research on the theoretical guarantees of VM-PG with different metric selections. However, most such metric selections are dependent on (an expensive) Hessian, or limited to scalar stepsizes like the Barzilai-Borwein (BB) stepsize with lots of safeguarding. Instead, in this paper we propose an adaptive metric selection strategy called the diagonal Barzilai-Borwein (BB) stepsize. The proposed diagonal selection better captures the local geometry of the problem while keeping per-step computation cost similar to the scalar BB stepsize i.e. $O(n)$. Under this metric selection for VM-PG, the theoretical convergence is analyzed. Our empirical studies illustrate the improved convergence results under the proposed diagonal BB stepsize, specifically for ill-conditioned machine learning problems for both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge