Unsupervised representational learning with recognition-parametrised probabilistic models

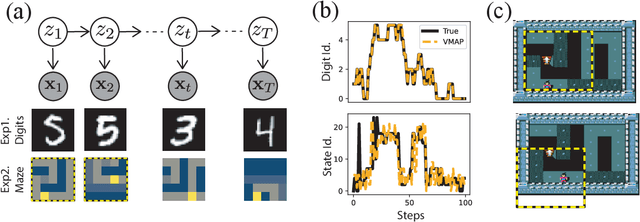
We introduce a new approach to probabilistic unsupervised learning based on the recognition-parametrised model (RPM): a normalised semi-parametric hypothesis class for joint distributions over observed and latent variables. Under the key assumption that observations are conditionally independent given the latents, RPMs directly encode the "recognition" process, parametrising both the prior distribution on the latents and their conditional distributions given observations. This recognition model is paired with non-parametric descriptions of the marginal distribution of each observed variable. Thus, the focus is on learning a good latent representation that captures dependence between the measurements. The RPM permits exact maximum likelihood learning in settings with discrete latents and a tractable prior, even when the mapping between continuous observations and the latents is expressed through a flexible model such as a neural network. We develop effective approximations for the case of continuous latent variables with tractable priors. Unlike the approximations necessary in dual-parametrised models such as Helmholtz machines and variational autoencoders, these RPM approximations introduce only minor bias, which may often vanish asymptotically. Furthermore, where the prior on latents is intractable the RPM may be combined effectively with standard probabilistic techniques such as variational Bayes. We demonstrate the model in high dimensional data settings, including a form of weakly supervised learning on MNIST digits and the discovery of latent maps from sensory observations. The RPM provides an effective way to discover, represent and reason probabilistically about the latent structure underlying observational data, functions which are critical to both animal and artificial intelligence.