Unsupervised Learning for Nonlinear PieceWise Smooth Hybrid Systems

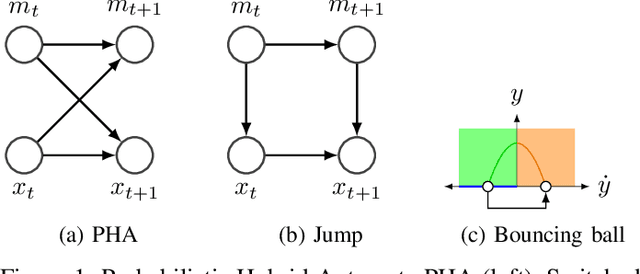
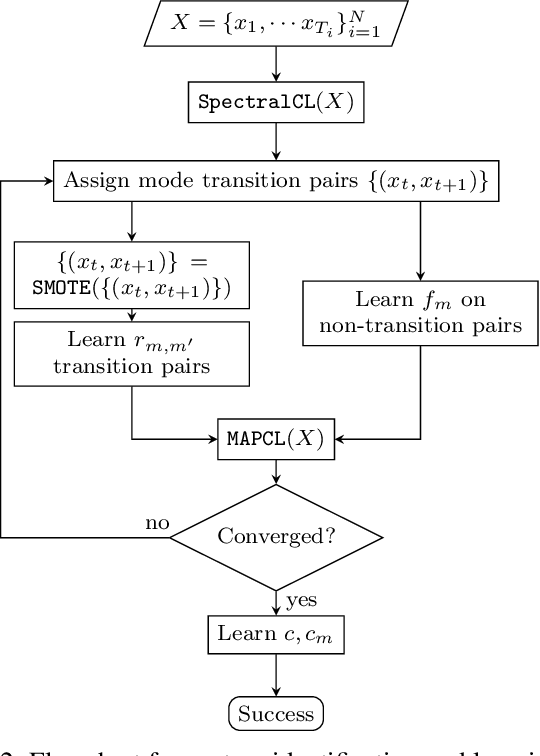
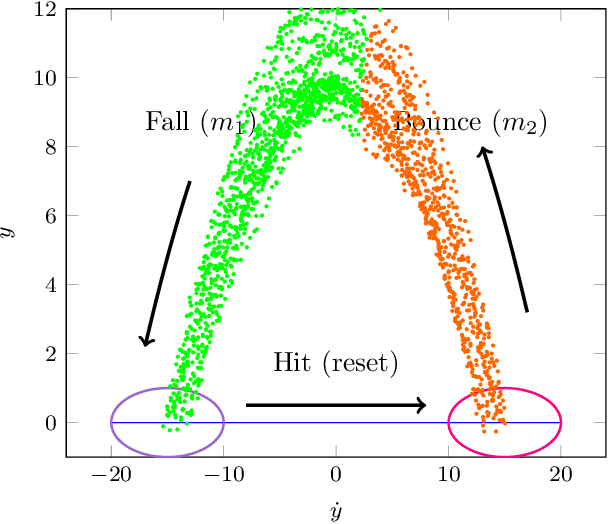
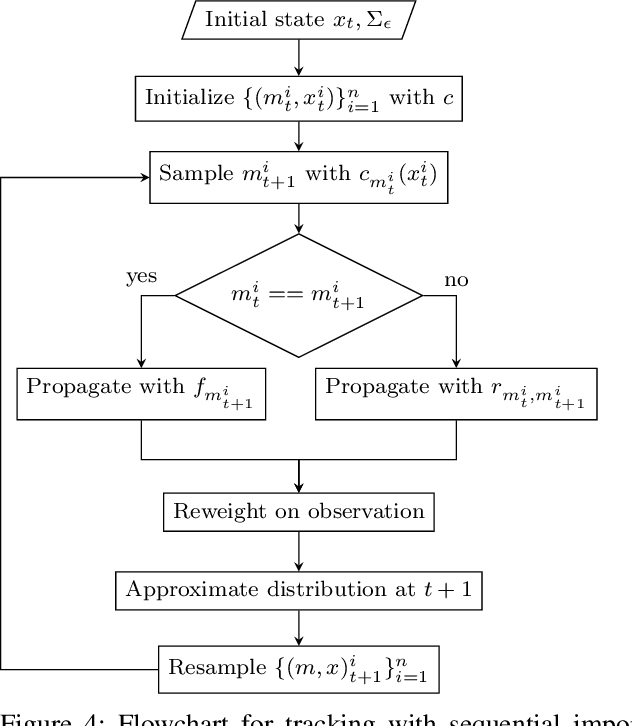
This paper introduces a novel system identification and tracking method for PieceWise Smooth (PWS) nonlinear stochastic hybrid systems. We are able to correctly identify and track challenging problems with diverse dynamics and low dimensional transitions. We exploit the composite structure system to learn a simpler model on each component/mode. We use Gaussian Process Regression techniques to learn smooth, nonlinear manifolds across mode transitions, guard-regions, and make multi-step ahead predictions on each mode dynamics. We combine a PWS non-linear model with a particle filter to effectively track multi-modal transitions. We further use synthetic oversampling techniques to address the challenge of detecting mode transition which is sparse compared to mode dynamics. This work provides an effective form of model learning in a complex hybrid system, which can be useful for future integration in a reinforcement learning setting. We compare multi-step prediction and tracking performance against traditional dynamical system tracking methods, such as EKF and Switching Gaussian Processes, and show that this framework performs significantly better, being able to correctly track complex dynamics with sparse transitions.