Understanding the Effects of Adversarial Personalized Ranking Optimization Method on Recommendation Quality
Paper and Code
Jul 29, 2021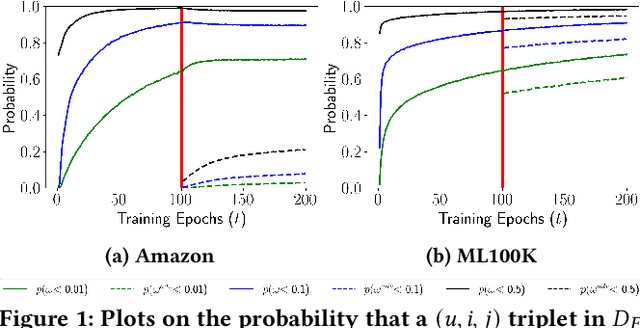
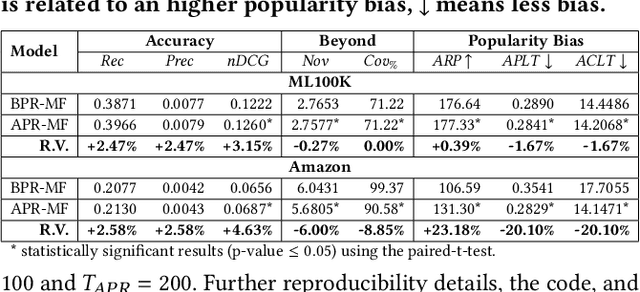
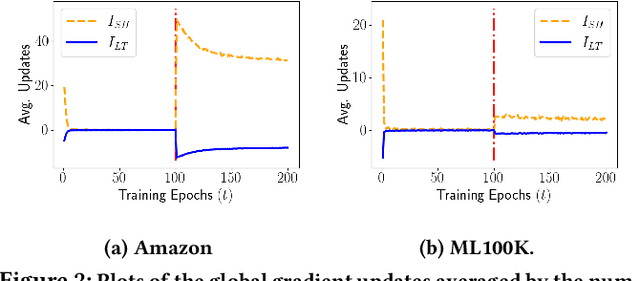
Recommender systems (RSs) employ user-item feedback, e.g., ratings, to match customers to personalized lists of products. Approaches to top-k recommendation mainly rely on Learning-To-Rank algorithms and, among them, the most widely adopted is Bayesian Personalized Ranking (BPR), which bases on a pair-wise optimization approach. Recently, BPR has been found vulnerable against adversarial perturbations of its model parameters. Adversarial Personalized Ranking (APR) mitigates this issue by robustifying BPR via an adversarial training procedure. The empirical improvements of APR's accuracy performance on BPR have led to its wide use in several recommender models. However, a key overlooked aspect has been the beyond-accuracy performance of APR, i.e., novelty, coverage, and amplification of popularity bias, considering that recent results suggest that BPR, the building block of APR, is sensitive to the intensification of biases and reduction of recommendation novelty. In this work, we model the learning characteristics of the BPR and APR optimization frameworks to give mathematical evidence that, when the feedback data have a tailed distribution, APR amplifies the popularity bias more than BPR due to an unbalanced number of received positive updates from short-head items. Using matrix factorization (MF), we empirically validate the theoretical results by performing preliminary experiments on two public datasets to compare BPR-MF and APR-MF performance on accuracy and beyond-accuracy metrics. The experimental results consistently show the degradation of novelty and coverage measures and a worrying amplification of bias.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge