Understanding Edge-of-Stability Training Dynamics with a Minimalist Example

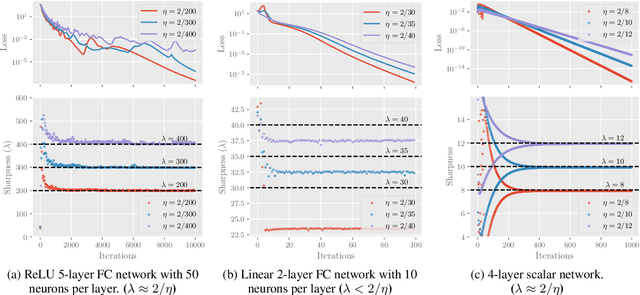
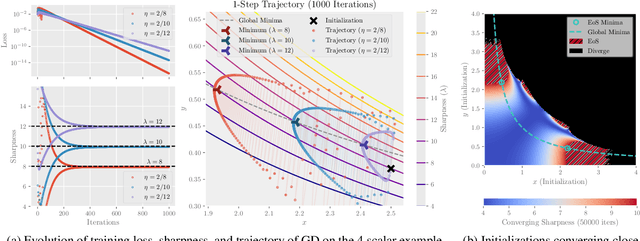
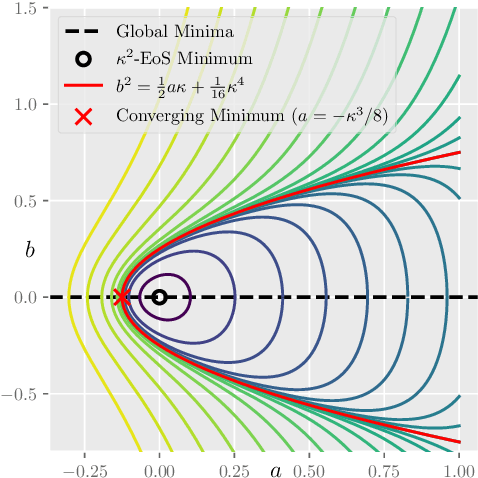
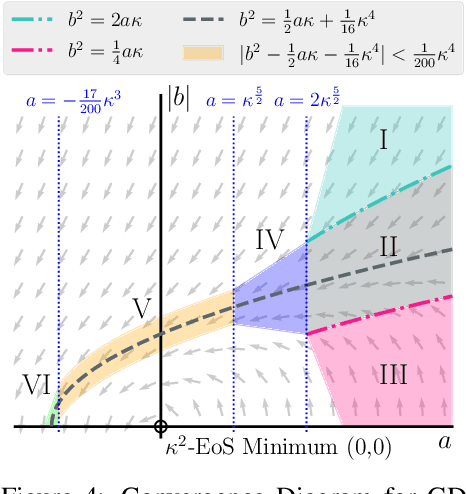
Recently, researchers observed that gradient descent for deep neural networks operates in an ``edge-of-stability'' (EoS) regime: the sharpness (maximum eigenvalue of the Hessian) is often larger than stability threshold 2/$\eta$ (where $\eta$ is the step size). Despite this, the loss oscillates and converges in the long run, and the sharpness at the end is just slightly below $2/\eta$. While many other well-understood nonconvex objectives such as matrix factorization or two-layer networks can also converge despite large sharpness, there is often a larger gap between sharpness of the endpoint and $2/\eta$. In this paper, we study EoS phenomenon by constructing a simple function that has the same behavior. We give rigorous analysis for its training dynamics in a large local region and explain why the final converging point has sharpness close to $2/\eta$. Globally we observe that the training dynamics for our example has an interesting bifurcating behavior, which was also observed in the training of neural nets.