Understanding Convolutional Neural Network Training with Information Theory

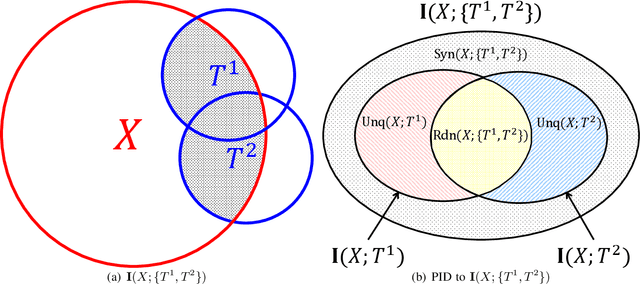
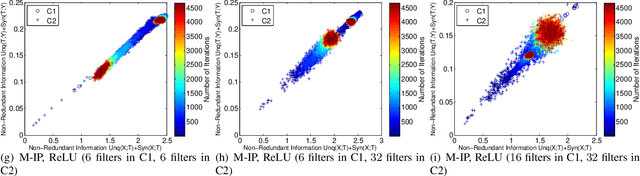
Using information theoretic concepts to understand and explore the inner organization of deep neural networks (DNNs) remains a big challenge. Recently, the concept of an information plane (coupled with the famed information bottleneck principle) began to shed light on the analysis of multilayer perceptrons (MLPs). We provided an in-depth insight into stacked autoencoders (SAEs) using a novel matrix-based Renyi's {\alpha}-entropy functional, enabling for the first time the analysis of the dynamics of learning using information flow in the real-world scenario involving complex network architecture and large data. Despite the great potential of these past works, there are several open questions when it comes to applying information theoretic concepts to understand convolutional neural networks (CNNs). These include for instance the accurate estimation of information quantities among multiple variables, and the many different training methodologies. By extending the novel matrix-based Renyi's {\alpha}-entropy functional to a multivariate scenario and introducing the partial information decomposition (PID) framework, this paper presents a systematic method to analyze CNNs training using information theory. Our results validate two fundamental data processing inequalities in CNNs, and also reveals some fundamental issues embedded in the training phase of CNNs.