Uncoupled Learning Dynamics with $O(\log T)$ Swap Regret in Multiplayer Games
Paper and Code
Apr 25, 2022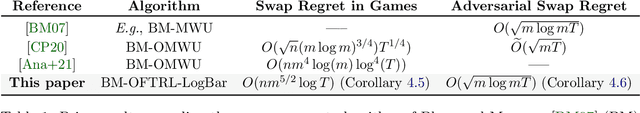
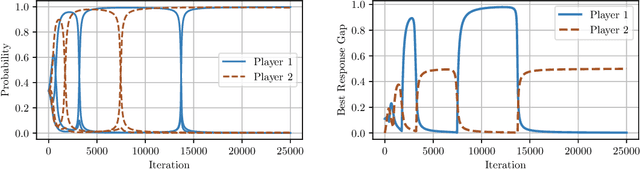
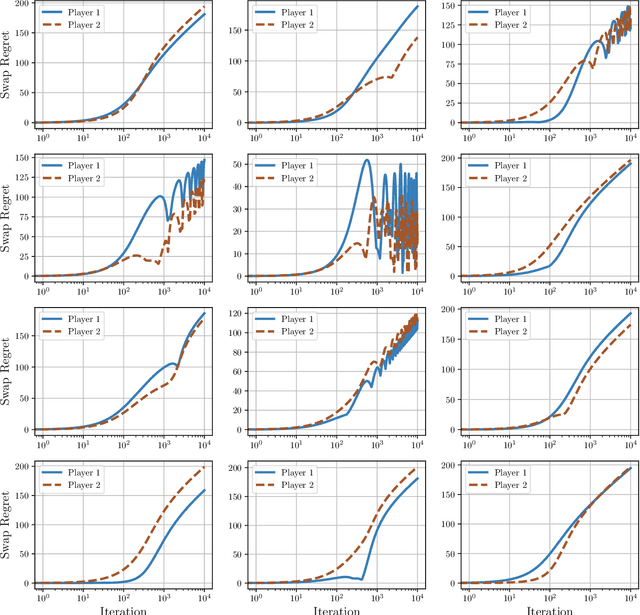
In this paper we establish efficient and \emph{uncoupled} learning dynamics so that, when employed by all players in a general-sum multiplayer game, the \emph{swap regret} of each player after $T$ repetitions of the game is bounded by $O(\log T)$, improving over the prior best bounds of $O(\log^4 (T))$. At the same time, we guarantee optimal $O(\sqrt{T})$ swap regret in the adversarial regime as well. To obtain these results, our primary contribution is to show that when all players follow our dynamics with a \emph{time-invariant} learning rate, the \emph{second-order path lengths} of the dynamics up to time $T$ are bounded by $O(\log T)$, a fundamental property which could have further implications beyond near-optimally bounding the (swap) regret. Our proposed learning dynamics combine in a novel way \emph{optimistic} regularized learning with the use of \emph{self-concordant barriers}. Further, our analysis is remarkably simple, bypassing the cumbersome framework of higher-order smoothness recently developed by Daskalakis, Fishelson, and Golowich (NeurIPS'21).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge