UAV Aided Over-the-Air Computation
Paper and Code
Jun 01, 2021


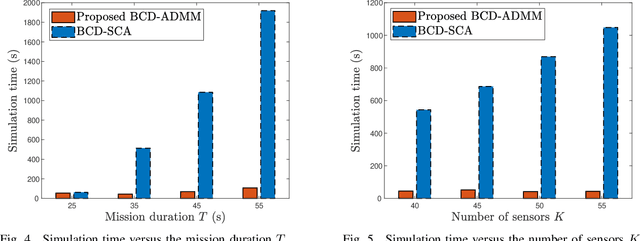
Over-the-air computation (AirComp) seamlessly integrates communication and computation by exploiting the waveform superposition property of multiple-access channels. Different from the existing works that focus on transceiver design of AirComp over static networks, this paper considers an unmanned aerial vehicle (UAV) aided AirComp system, where the UAV as a flying base station aggregates data from mobile sensors. The trajectory design of the UAV provides an additional degree of freedom to improve the performance of AirComp. Our goal is to minimize the time-averaged mean-squared error (MSE) of AirComp by jointly optimizing the UAV trajectory, receive normalizing factors, and sensors' transmit power. To this end, we first propose a novel and equivalent problem transformation by introducing intermediate variables. This reformulation leads to a convex subproblem when fixing any other two blocks of variables, thereby enabling efficient algorithm design based on the principle of block coordinate descent and alternating direction method of multipliers (ADMM) techniques. In particular, we derive the optimal closed-form solutions for normalizing factors and intermediate variables optimization subproblems. We also recast the convex trajectory design subproblem into an ADMM form and obtain the closed-form expressions for each variable updating. Simulation results show that the proposed algorithm achieves a smaller time-averaged MSE while reducing the simulation time by orders of magnitude compared to state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge