Two-stage Denoising Diffusion Model for Source Localization in Graph Inverse Problems
Paper and Code
Apr 18, 2023

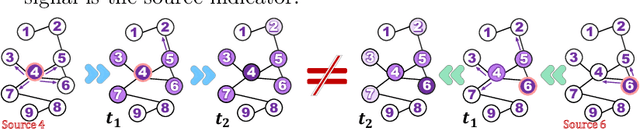

Source localization is the inverse problem of graph information dissemination and has broad practical applications. However, the inherent intricacy and uncertainty in information dissemination pose significant challenges, and the ill-posed nature of the source localization problem further exacerbates these challenges. Recently, deep generative models, particularly diffusion models inspired by classical non-equilibrium thermodynamics, have made significant progress. While diffusion models have proven to be powerful in solving inverse problems and producing high-quality reconstructions, applying them directly to the source localization is infeasible for two reasons. Firstly, it is impossible to calculate the posterior disseminated results on a large-scale network for iterative denoising sampling, which would incur enormous computational costs. Secondly, in the existing methods for this field, the training data itself are ill-posed (many-to-one); thus simply transferring the diffusion model would only lead to local optima. To address these challenges, we propose a two-stage optimization framework, the source localization denoising diffusion model (SL-Diff). In the coarse stage, we devise the source proximity degrees as the supervised signals to generate coarse-grained source predictions. This aims to efficiently initialize the next stage, significantly reducing its convergence time and calibrating the convergence process. Furthermore, the introduction of cascade temporal information in this training method transforms the many-to-one mapping relationship into a one-to-one relationship, perfectly addressing the ill-posed problem. In the fine stage, we design a diffusion model for the graph inverse problem that can quantify the uncertainty in the dissemination. The proposed SL-Diff yields excellent prediction results within a reasonable sampling time at extensive experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge