Traversing the Local Polytopes of ReLU Neural Networks: A Unified Approach for Network Verification

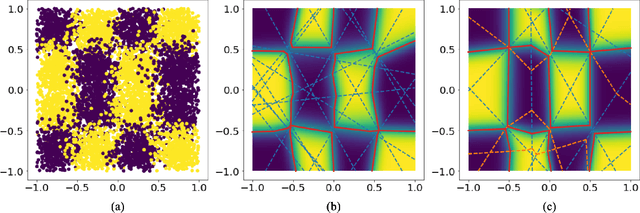
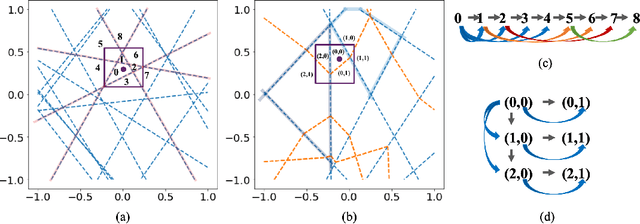
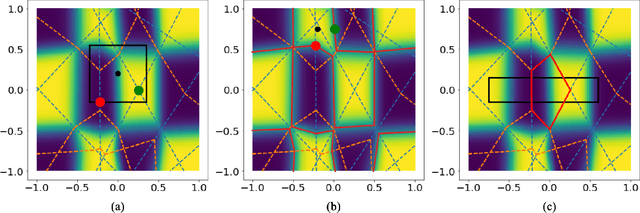
Although neural networks (NNs) with ReLU activation functions have found success in a wide range of applications, their adoption in risk-sensitive settings has been limited by the concerns on robustness and interpretability. Previous works to examine robustness and to improve interpretability partially exploited the piecewise linear function form of ReLU NNs. In this paper, we explore the unique topological structure that ReLU NNs create in the input space, identifying the adjacency among the partitioned local polytopes and developing a traversing algorithm based on this adjacency. Our polytope traversing algorithm can be adapted to verify a wide range of network properties related to robustness and interpretability, providing an unified approach to examine the network behavior. As the traversing algorithm explicitly visits all local polytopes, it returns a clear and full picture of the network behavior within the traversed region. The time and space complexity of the traversing algorithm is determined by the number of a ReLU NN's partitioning hyperplanes passing through the traversing region.