Training-Free Robust Multimodal Learning via Sample-Wise Jacobian Regularization
Paper and Code
Apr 05, 2022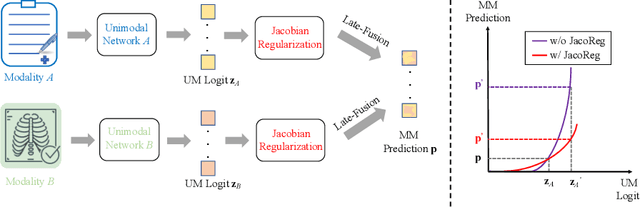
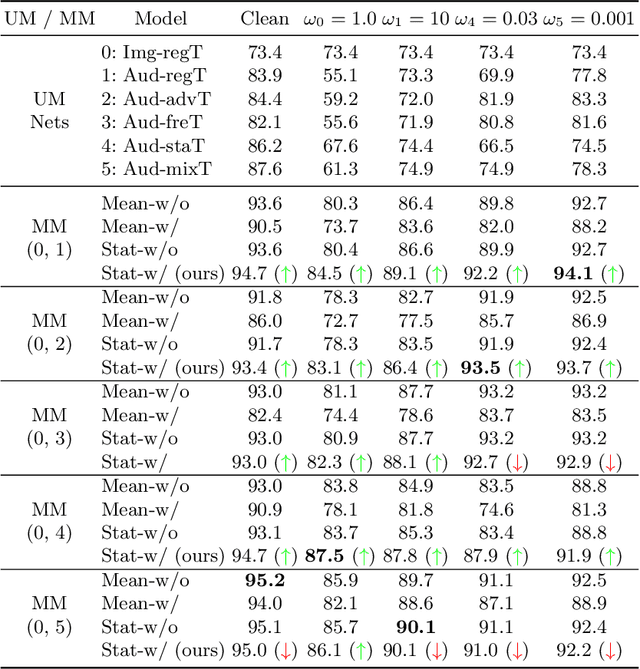
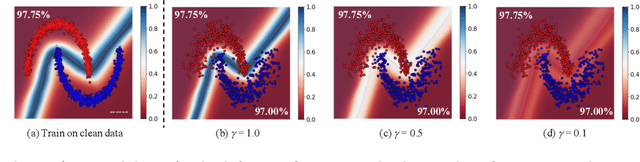
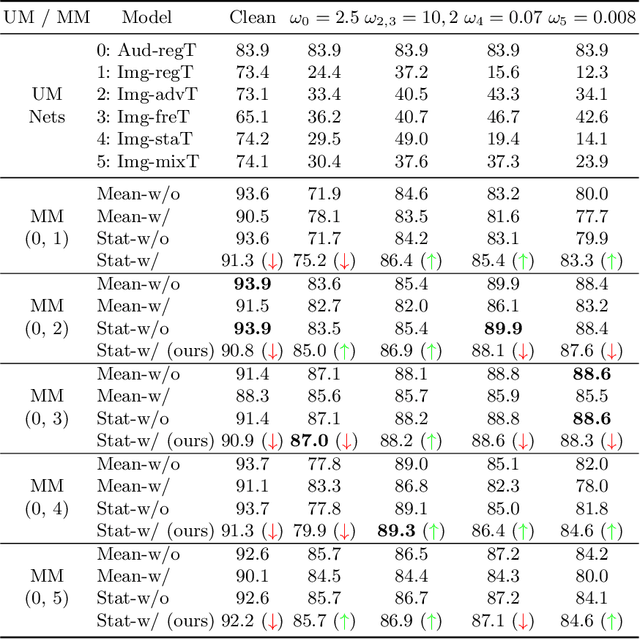
Multimodal fusion emerges as an appealing technique to improve model performances on many tasks. Nevertheless, the robustness of such fusion methods is rarely involved in the present literature. In this paper, we propose a training-free robust late-fusion method by exploiting conditional independence assumption and Jacobian regularization. Our key is to minimize the Frobenius norm of a Jacobian matrix, where the resulting optimization problem is relaxed to a tractable Sylvester equation. Furthermore, we provide a theoretical error bound of our method and some insights about the function of the extra modality. Several numerical experiments on AV-MNIST, RAVDESS, and VGGsound demonstrate the efficacy of our method under both adversarial attacks and random corruptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge