Trainable Weight Averaging for Fast Convergence and Better Generalization

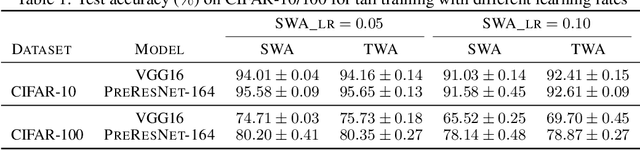
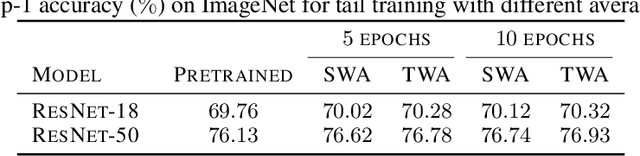
Stochastic gradient descent (SGD) and its variants are commonly considered as the de-facto methods to train deep neural networks (DNNs). While recent improvements to SGD mainly focus on the descent algorithm itself, few works pay attention to utilizing the historical solutions -- as an iterative method, SGD has actually gone through substantial explorations before its final convergence. Recently, an interesting attempt is stochastic weight averaging (SWA), which significantly improves the generalization by simply averaging the solutions at the tail stage of training. In this paper, we propose to optimize the averaging coefficients, leading to our Trainable Weight Averaging (TWA), essentially a novel training method in a reduced subspace spanned by historical solutions. TWA is quite efficient and has good generalization capability as the degree of freedom for training is small. It largely reduces the estimation error from SWA, making it not only further improve the SWA solutions but also take full advantage of the solutions generated in the head of training where SWA fails. In the extensive numerical experiments, (i) TWA achieves consistent improvements over SWA with less sensitivity to learning rate; (ii) applying TWA in the head stage of training largely speeds up the convergence, resulting in over 40% time saving on CIFAR and 30% on ImageNet with improved generalization compared with regular training. The code is released at https://github.com/nblt/TWA.