Tradeoffs in Streaming Binary Classification under Limited Inspection Resources
Paper and Code
Oct 05, 2021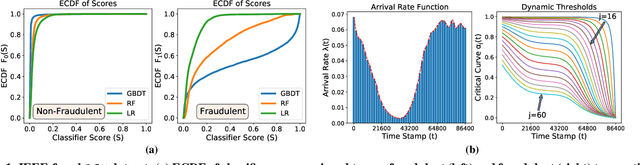

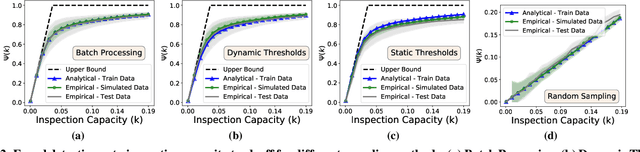

Institutions are increasingly relying on machine learning models to identify and alert on abnormal events, such as fraud, cyber attacks and system failures. These alerts often need to be manually investigated by specialists. Given the operational cost of manual inspections, the suspicious events are selected by alerting systems with carefully designed thresholds. In this paper, we consider an imbalanced binary classification problem, where events arrive sequentially and only a limited number of suspicious events can be inspected. We model the event arrivals as a non-homogeneous Poisson process, and compare various suspicious event selection methods including those based on static and adaptive thresholds. For each method, we analytically characterize the tradeoff between the minority-class detection rate and the inspection capacity as a function of the data class imbalance and the classifier confidence score densities. We implement the selection methods on a real public fraud detection dataset and compare the empirical results with analytical bounds. Finally, we investigate how class imbalance and the choice of classifier impact the tradeoff.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge