Towards Understanding the Condensation of Two-layer Neural Networks at Initial Training

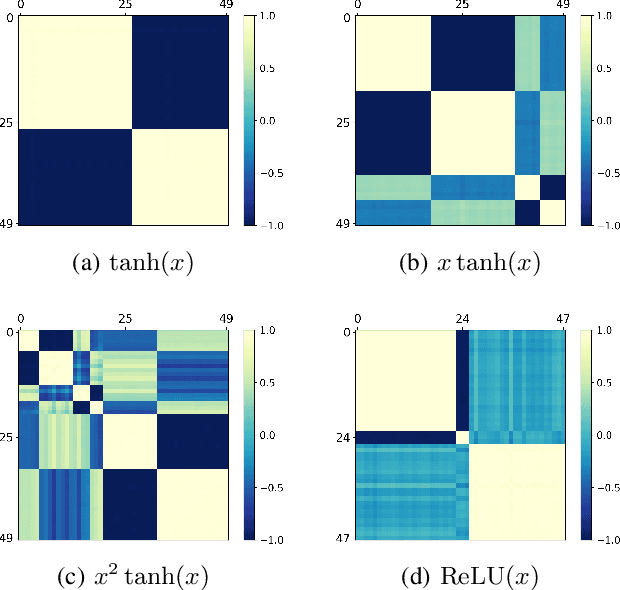
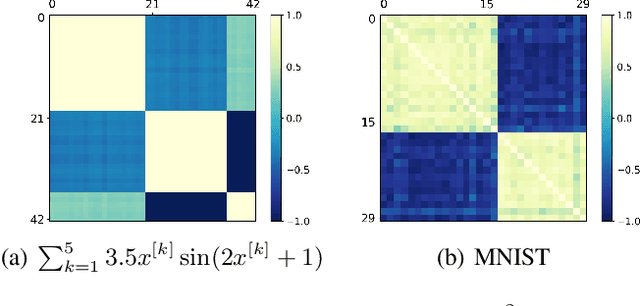
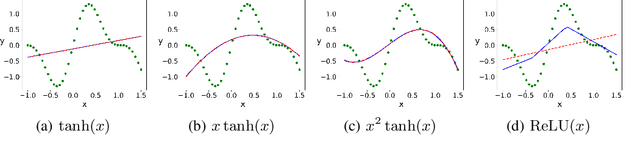
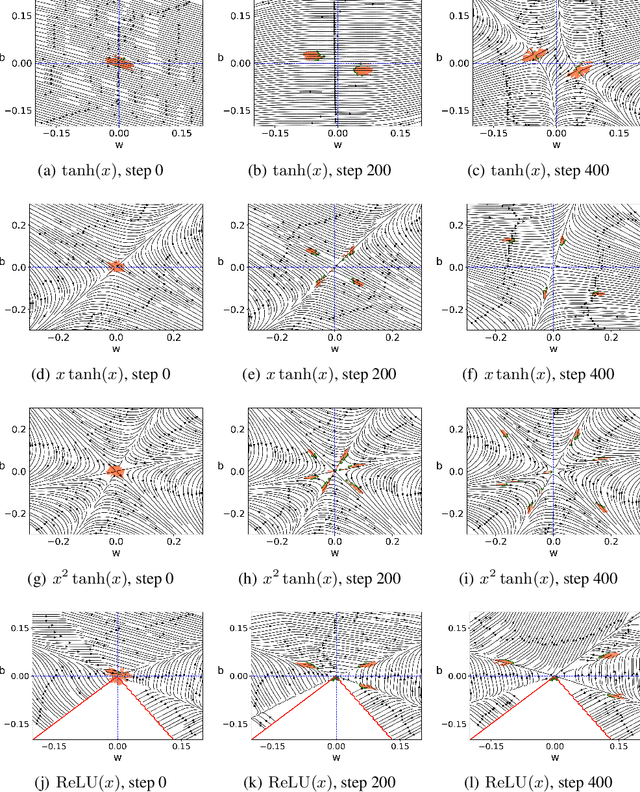
It is important to study what implicit regularization is imposed on the loss function during the training that leads over-parameterized neural networks (NNs) to good performance on real dataset. Empirically, existing works have shown that weights of NNs condense on isolated orientations with small initialization. The condensation implies that the NN learns features from the training data and is effectively a much smaller network. In this work, we show that the singularity of the activation function at original point is a key factor to understanding the condensation at initial training stage. Our experiments suggest that the maximal number of condensed orientations is twice of the singularity order. Our theoretical analysis confirms experiments for two cases, one is for the first-order singularity activation function and the other is for the one-dimensional input. This work takes a step towards understanding how small initialization implicitly leads NNs to condensation at initial training, which is crucial to understand the training and the learning of deep NNs.