Towards Tractable Mathematical Reasoning: Challenges, Strategies, and Opportunities for Solving Math Word Problems
Paper and Code
Oct 29, 2021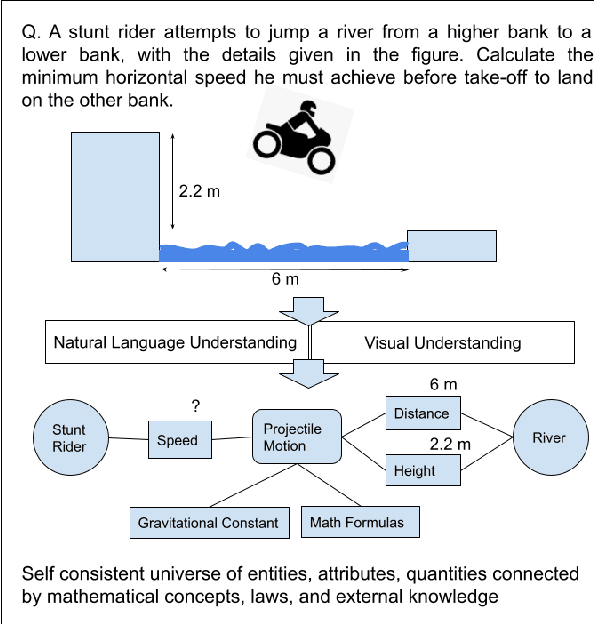

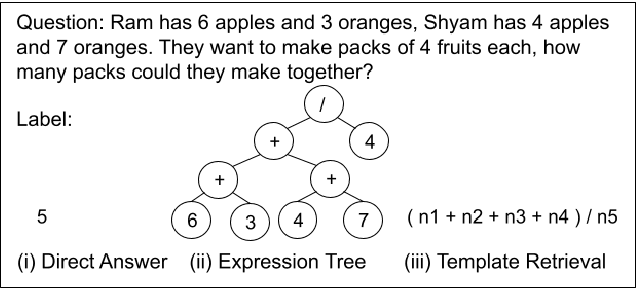
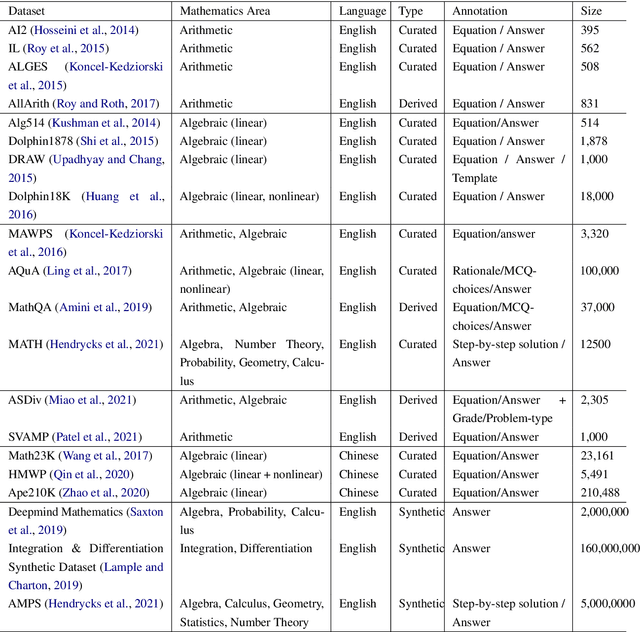
Mathematical reasoning would be one of the next frontiers for artificial intelligence to make significant progress. The ongoing surge to solve math word problems (MWPs) and hence achieve better mathematical reasoning ability would continue to be a key line of research in the coming time. We inspect non-neural and neural methods to solve math word problems narrated in a natural language. We also highlight the ability of these methods to be generalizable, mathematically reasonable, interpretable, and explainable. Neural approaches dominate the current state of the art, and we survey them highlighting three strategies to MWP solving: (1) direct answer generation, (2) expression tree generation for inferring answers, and (3) template retrieval for answer computation. Moreover, we discuss technological approaches, review the evolution of intuitive design choices to solve MWPs, and examine them for mathematical reasoning ability. We finally identify several gaps that warrant the need for external knowledge and knowledge-infused learning, among several other opportunities in solving MWPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge