Towards Stable, Globally Expressive Graph Representations with Laplacian Eigenvectors

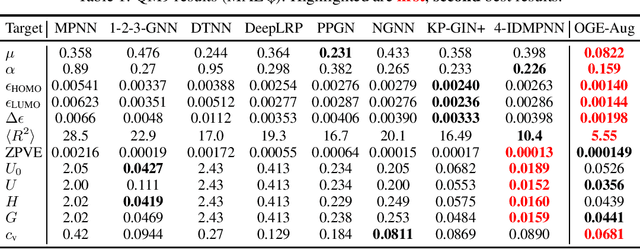
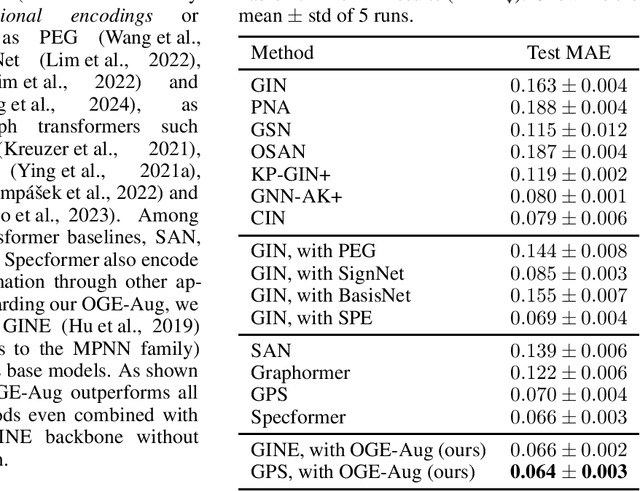
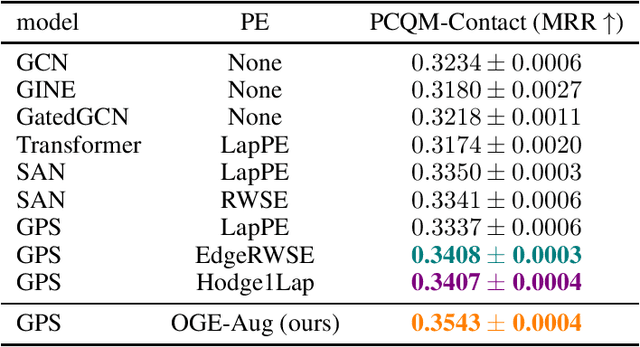
Graph neural networks (GNNs) have achieved remarkable success in a variety of machine learning tasks over graph data. Existing GNNs usually rely on message passing, i.e., computing node representations by gathering information from the neighborhood, to build their underlying computational graphs. They are known fairly limited in expressive power, and often fail to capture global characteristics of graphs. To overcome the issue, a popular solution is to use Laplacian eigenvectors as additional node features, as they contain global positional information of nodes, and can serve as extra node identifiers aiding GNNs to separate structurally similar nodes. For such an approach, properly handling the orthogonal group symmetry among eigenvectors with equal eigenvalue is crucial for its stability and generalizability. However, using a naive orthogonal group invariant encoder for each separate eigenspace may not keep the full expressivity in the Laplacian eigenvectors. Moreover, computing such invariants inevitably entails a hard split of Laplacian eigenvalues according to their numerical identity, which suffers from great instability when the graph structure is perturbed. In this paper, we propose a novel method exploiting Laplacian eigenvectors to generate stable and globally expressive graph representations. The main difference from previous works is that (i) our method utilizes learnable orthogonal group invariant representations for each Laplacian eigenspace, based upon powerful orthogonal group equivariant neural network layers already well studied in the literature, and that (ii) our method deals with numerically close eigenvalues in a smooth fashion, ensuring its better robustness against perturbations. Experiments on various graph learning benchmarks witness the competitive performance of our method, especially its great potential to learn global properties of graphs.