Towards Probabilistic Tensor Canonical Polyadic Decomposition 2.0: Automatic Tensor Rank Learning Using Generalized Hyperbolic Prior

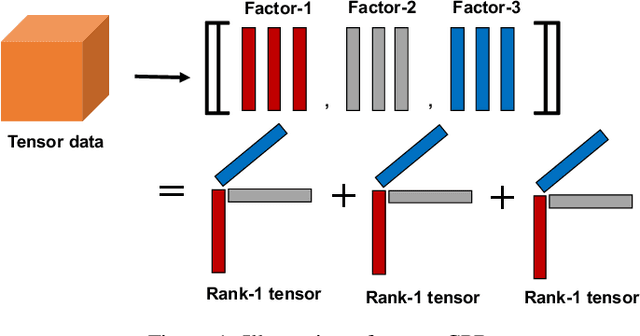
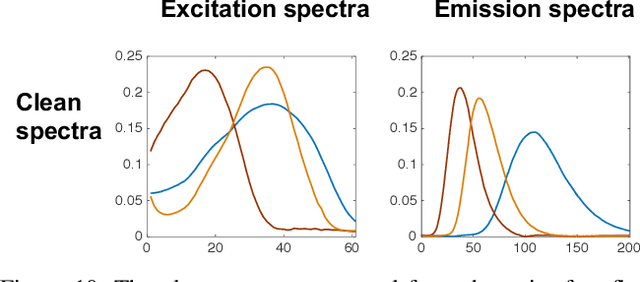
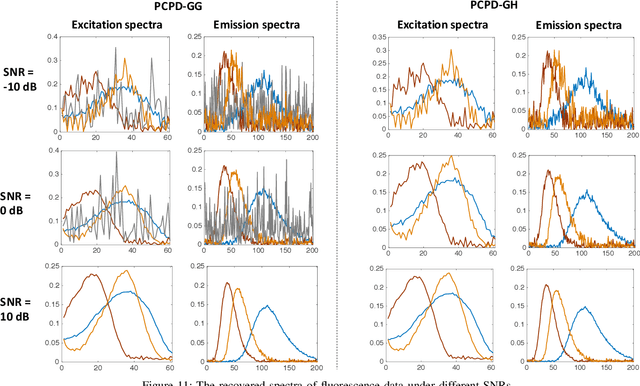
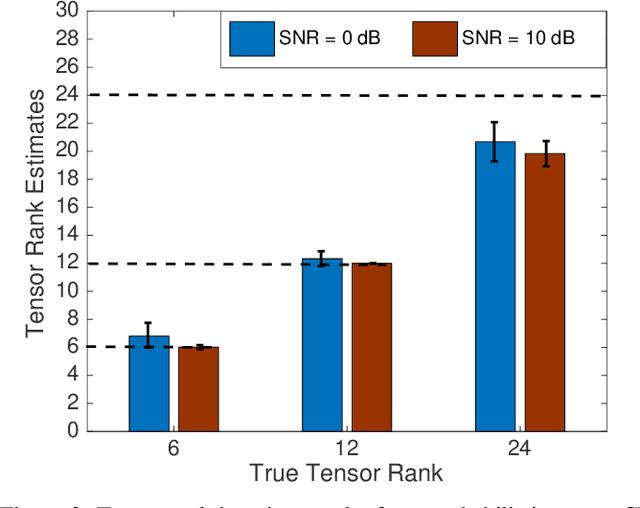
Tensor rank learning for canonical polyadic decomposition (CPD) has long been deemed as an essential but challenging problem. In particular, since the tensor rank controls the complexity of the CPD model, its inaccurate learning would cause overfitting to noise or underfitting to the signal sources, and even destroy the interpretability of model parameters. However, the optimal determination of a tensor rank is known to be a non-deterministic polynomial-time hard (NP-hard) task. Rather than exhaustively searching for the best tensor rank via trial-and-error experiments, Bayesian inference under the Gaussian-gamma prior was introduced in the context of probabilistic CPD modeling and it was shown to be an effective strategy for automatic tensor rank determination. This triggered flourishing research on other structured tensor CPDs with automatic tensor rank learning. As the other side of the coin, these research works also reveal that the Gaussian-gamma model does not perform well for high-rank tensors or/and low signal-to-noise ratios (SNRs). To overcome these drawbacks, in this paper, we introduce a more advanced generalized hyperbolic (GH) prior to the probabilistic CPD model, which not only includes the Gaussian-gamma model as a special case, but also provides more flexibilities to adapt to different levels of sparsity. Based on this novel probabilistic model, an algorithm is developed under the framework of variational inference, where each update is obtained in a closed-form. Extensive numerical results, using synthetic data and real-world datasets, demonstrate the excellent performance of the proposed method in learning both low as well as high tensor ranks even for low SNR cases.