Towards Certification of Uncertainty Calibration under Adversarial Attacks
Paper and Code
May 22, 2024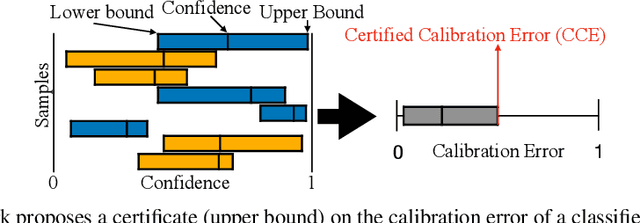
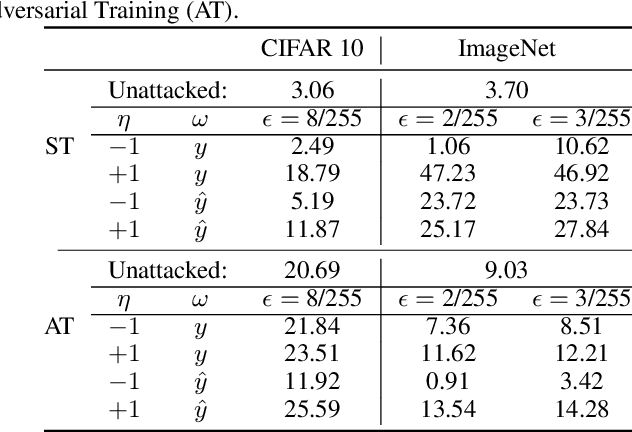
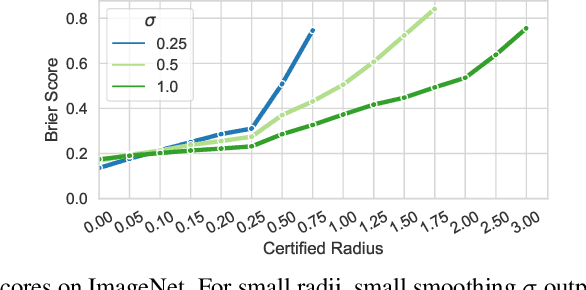
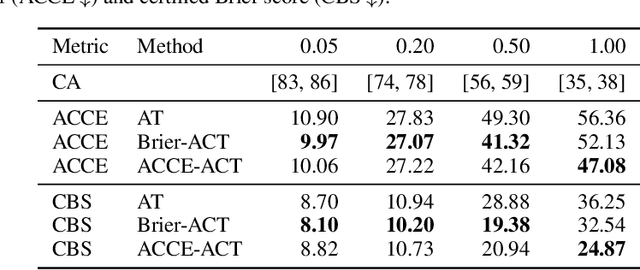
Since neural classifiers are known to be sensitive to adversarial perturbations that alter their accuracy, \textit{certification methods} have been developed to provide provable guarantees on the insensitivity of their predictions to such perturbations. Furthermore, in safety-critical applications, the frequentist interpretation of the confidence of a classifier (also known as model calibration) can be of utmost importance. This property can be measured via the Brier score or the expected calibration error. We show that attacks can significantly harm calibration, and thus propose certified calibration as worst-case bounds on calibration under adversarial perturbations. Specifically, we produce analytic bounds for the Brier score and approximate bounds via the solution of a mixed-integer program on the expected calibration error. Finally, we propose novel calibration attacks and demonstrate how they can improve model calibration through \textit{adversarial calibration training}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge