TLINet: Differentiable Neural Network Temporal Logic Inference
Paper and Code
May 14, 2024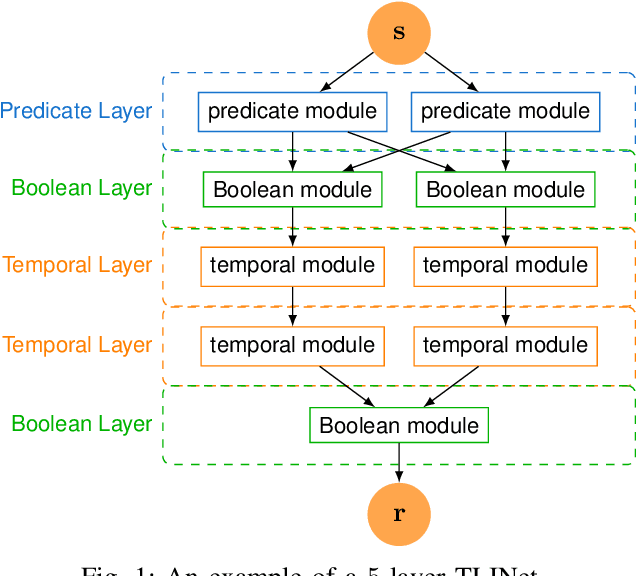
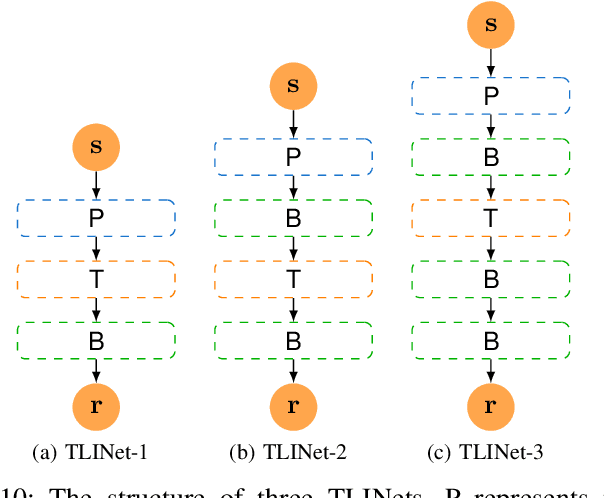
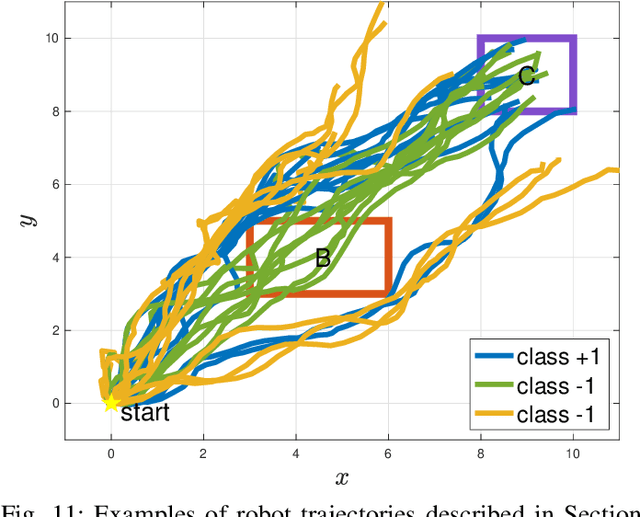
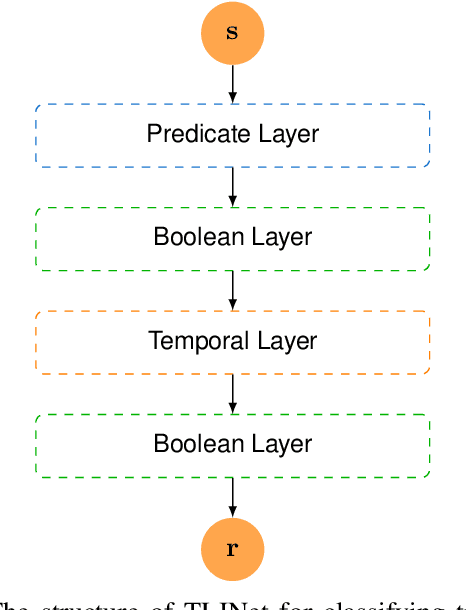
There has been a growing interest in extracting formal descriptions of the system behaviors from data. Signal Temporal Logic (STL) is an expressive formal language used to describe spatial-temporal properties with interpretability. This paper introduces TLINet, a neural-symbolic framework for learning STL formulas. The computation in TLINet is differentiable, enabling the usage of off-the-shelf gradient-based tools during the learning process. In contrast to existing approaches, we introduce approximation methods for max operator designed specifically for temporal logic-based gradient techniques, ensuring the correctness of STL satisfaction evaluation. Our framework not only learns the structure but also the parameters of STL formulas, allowing flexible combinations of operators and various logical structures. We validate TLINet against state-of-the-art baselines, demonstrating that our approach outperforms these baselines in terms of interpretability, compactness, rich expressibility, and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge