Thoughts on the Consistency between Ricci Flow and Neural Network Behavior

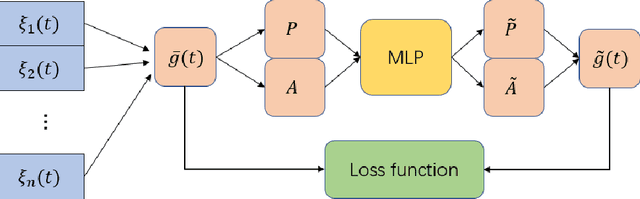
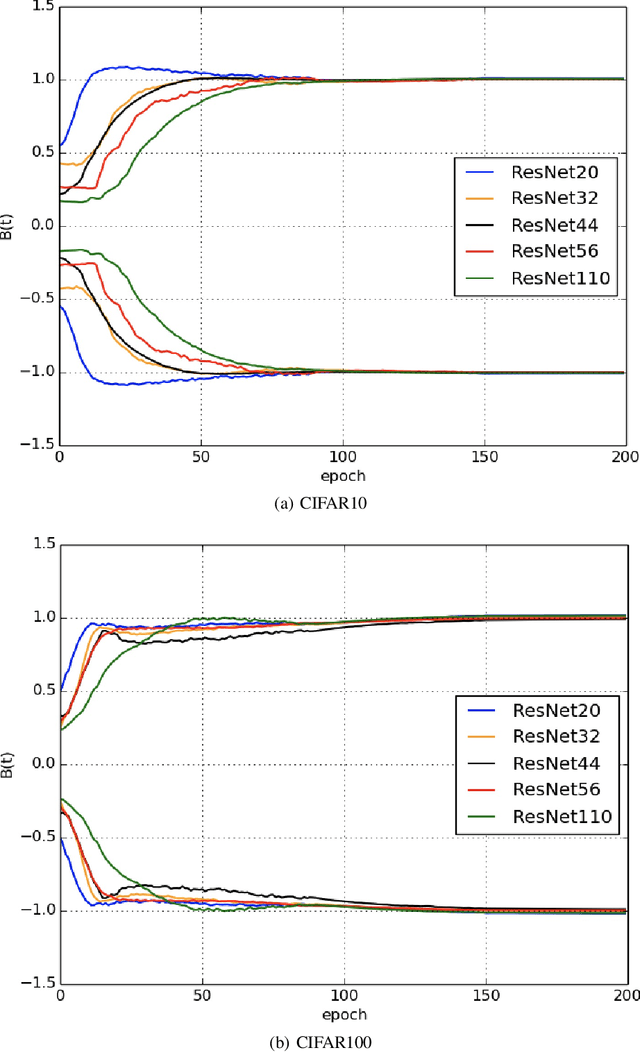
The Ricci flow is a partial differential equation for evolving the metric in a Riemannian manifold to make it more regular. However, in most cases, the Ricci flow tends to develop singularities and lead to divergence of the solution. In this paper, we propose the linearly nearly Euclidean metric to assist manifold micro-surgery, which means that we prove the dynamical stability and convergence of the metrics close to the linearly nearly Euclidean metric under the Ricci-DeTurck flow. In practice, from the information geometry and mirror descent points of view, we give the steepest descent gradient flow for neural networks on the linearly nearly Euclidean manifold. During the training process of the neural network, we observe that its metric will also regularly converge to the linearly nearly Euclidean metric, which is consistent with the convergent behavior of linearly nearly Euclidean manifolds under Ricci-DeTurck flow.