The Recurrent Neural Tangent Kernel

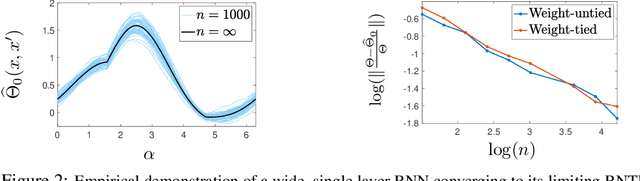
The study of deep networks (DNs) in the infinite-width limit, via the so-called Neural Tangent Kernel (NTK) approach, has provided new insights into the dynamics of learning, generalization, and the impact of initialization. One key DN architecture remains to be kernelized, namely, the Recurrent Neural Network (RNN). In this paper we introduce and study the Recurrent Neural Tangent Kernel (RNTK), which sheds new insights into the behavior of overparametrized RNNs, including how different time steps are weighted by the RNTK to form the output under different initialization parameters and nonlinearity choices, and how inputs of different lengths are treated. We demonstrate via a number of experiments that the RNTK offers significant performance gains over other kernels, including standard NTKs across a range of different data sets. A unique benefit of the RNTK is that it is agnostic to the length of the input, in stark contrast to other kernels.