The Impact of Mutation Rate on the Computation Time of Evolutionary Dynamic Optimization
Paper and Code
Jun 03, 2011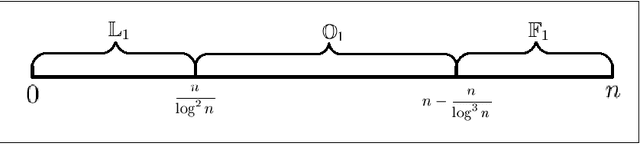
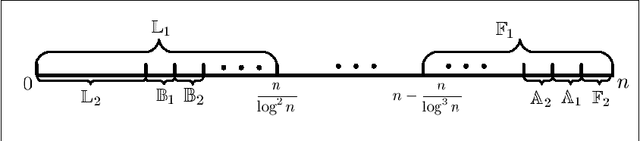
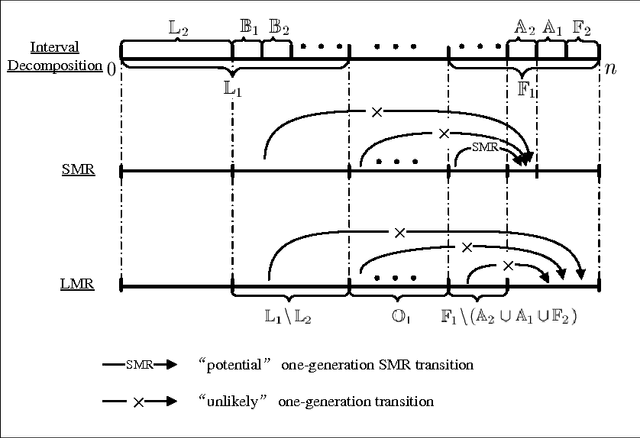
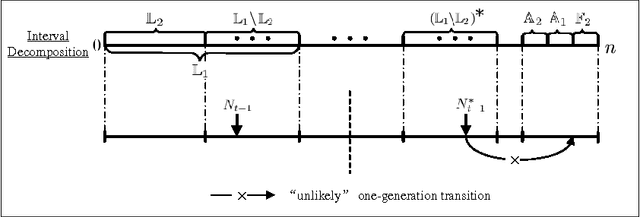
Mutation has traditionally been regarded as an important operator in evolutionary algorithms. In particular, there have been many experimental studies which showed the effectiveness of adapting mutation rates for various static optimization problems. Given the perceived effectiveness of adaptive and self-adaptive mutation for static optimization problems, there have been speculations that adaptive and self-adaptive mutation can benefit dynamic optimization problems even more since adaptation and self-adaptation are capable of following a dynamic environment. However, few theoretical results are available in analyzing rigorously evolutionary algorithms for dynamic optimization problems. It is unclear when adaptive and self-adaptive mutation rates are likely to be useful for evolutionary algorithms in solving dynamic optimization problems. This paper provides the first rigorous analysis of adaptive mutation and its impact on the computation times of evolutionary algorithms in solving certain dynamic optimization problems. More specifically, for both individual-based and population-based EAs, we have shown that any time-variable mutation rate scheme will not significantly outperform a fixed mutation rate on some dynamic optimization problem instances. The proofs also offer some insights into conditions under which any time-variable mutation scheme is unlikely to be useful and into the relationships between the problem characteristics and algorithmic features (e.g., different mutation schemes).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge