The Dog Walking Theory: Rethinking Convergence in Federated Learning
Paper and Code
Apr 18, 2024
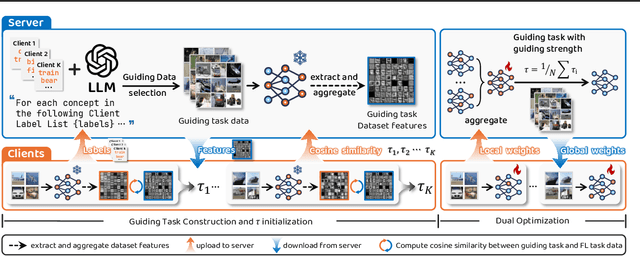
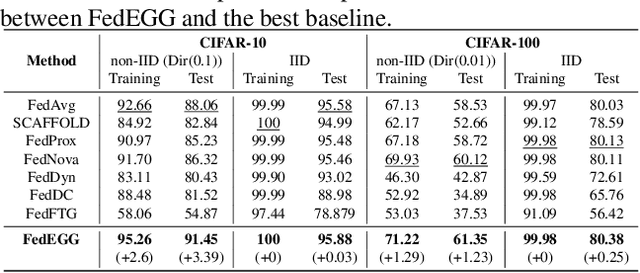
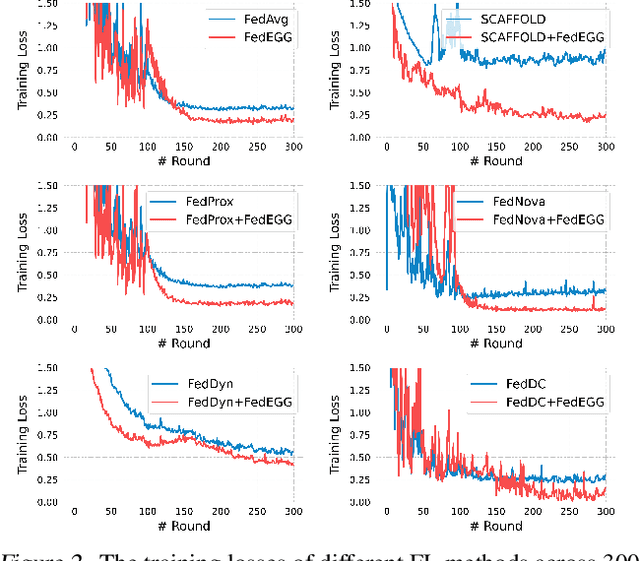
Federated learning (FL) is a collaborative learning paradigm that allows different clients to train one powerful global model without sharing their private data. Although FL has demonstrated promising results in various applications, it is known to suffer from convergence issues caused by the data distribution shift across different clients, especially on non-independent and identically distributed (non-IID) data. In this paper, we study the convergence of FL on non-IID data and propose a novel \emph{Dog Walking Theory} to formulate and identify the missing element in existing research. The Dog Walking Theory describes the process of a dog walker leash walking multiple dogs from one side of the park to the other. The goal of the dog walker is to arrive at the right destination while giving the dogs enough exercise (i.e., space exploration). In FL, the server is analogous to the dog walker while the clients are analogous to the dogs. This analogy allows us to identify one crucial yet missing element in existing FL algorithms: the leash that guides the exploration of the clients. To address this gap, we propose a novel FL algorithm \emph{FedWalk} that leverages an external easy-to-converge task at the server side as a \emph{leash task} to guide the local training of the clients. We theoretically analyze the convergence of FedWalk with respect to data heterogeneity (between server and clients) and task discrepancy (between the leash and the original tasks). Experiments on multiple benchmark datasets demonstrate the superiority of FedWalk over state-of-the-art FL methods under both IID and non-IID settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge