The Aleatoric Uncertainty Estimation Using a Separate Formulation with Virtual Residuals
Paper and Code
Nov 03, 2020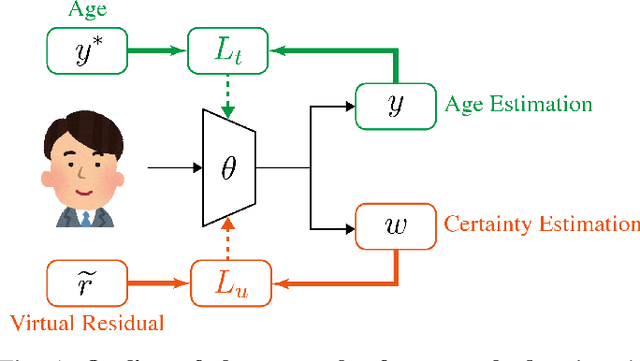
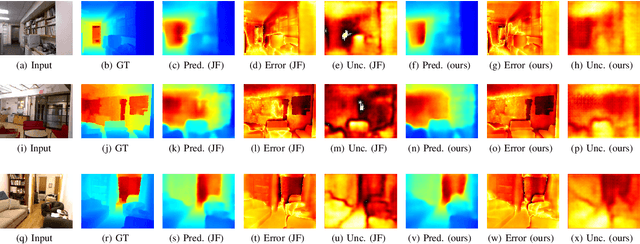
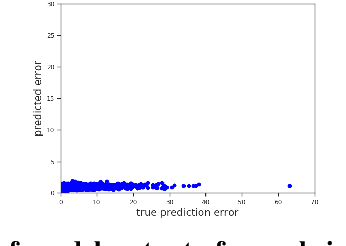
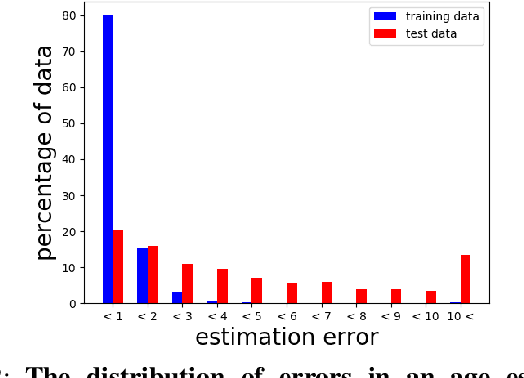
We propose a new optimization framework for aleatoric uncertainty estimation in regression problems. Existing methods can quantify the error in the target estimation, but they tend to underestimate it. To obtain the predictive uncertainty inherent in an observation, we propose a new separable formulation for the estimation of a signal and of its uncertainty, avoiding the effect of overfitting. By decoupling target estimation and uncertainty estimation, we also control the balance between signal estimation and uncertainty estimation. We conduct three types of experiments: regression with simulation data, age estimation, and depth estimation. We demonstrate that the proposed method outperforms a state-of-the-art technique for signal and uncertainty estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge