TCT: Convexifying Federated Learning using Bootstrapped Neural Tangent Kernels
Paper and Code
Jul 13, 2022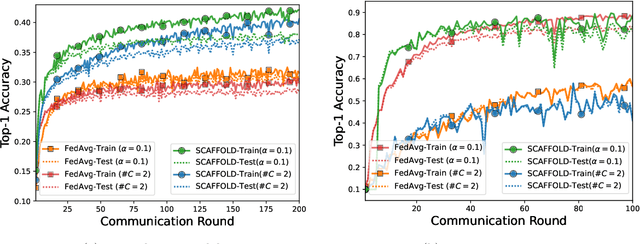
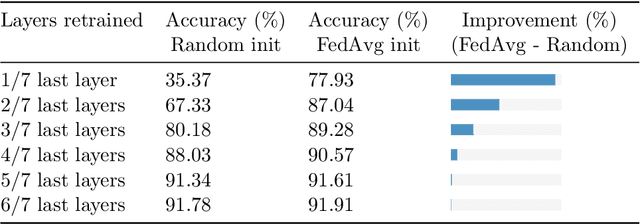

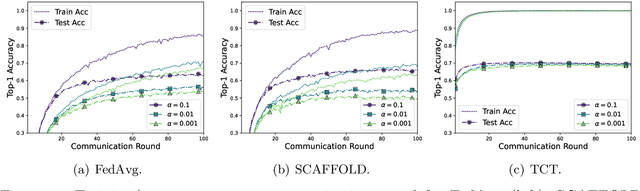
State-of-the-art federated learning methods can perform far worse than their centralized counterparts when clients have dissimilar data distributions. For neural networks, even when centralized SGD easily finds a solution that is simultaneously performant for all clients, current federated optimization methods fail to converge to a comparable solution. We show that this performance disparity can largely be attributed to optimization challenges presented by nonconvexity. Specifically, we find that the early layers of the network do learn useful features, but the final layers fail to make use of them. That is, federated optimization applied to this non-convex problem distorts the learning of the final layers. Leveraging this observation, we propose a Train-Convexify-Train (TCT) procedure to sidestep this issue: first, learn features using off-the-shelf methods (e.g., FedAvg); then, optimize a convexified problem obtained from the network's empirical neural tangent kernel approximation. Our technique yields accuracy improvements of up to +36% on FMNIST and +37% on CIFAR10 when clients have dissimilar data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge