TaylorGrid: Towards Fast and High-Quality Implicit Field Learning via Direct Taylor-based Grid Optimization

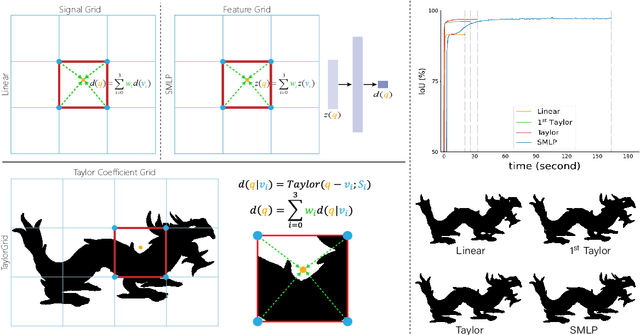
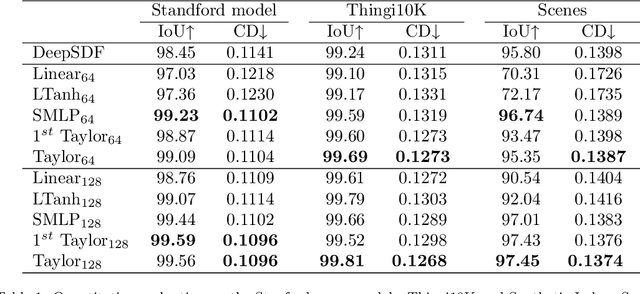
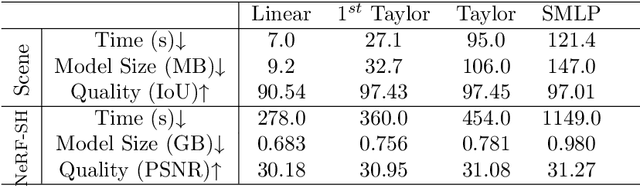
Coordinate-based neural implicit representation or implicit fields have been widely studied for 3D geometry representation or novel view synthesis. Recently, a series of efforts have been devoted to accelerating the speed and improving the quality of the coordinate-based implicit field learning. Instead of learning heavy MLPs to predict the neural implicit values for the query coordinates, neural voxels or grids combined with shallow MLPs have been proposed to achieve high-quality implicit field learning with reduced optimization time. On the other hand, lightweight field representations such as linear grid have been proposed to further improve the learning speed. In this paper, we aim for both fast and high-quality implicit field learning, and propose TaylorGrid, a novel implicit field representation which can be efficiently computed via direct Taylor expansion optimization on 2D or 3D grids. As a general representation, TaylorGrid can be adapted to different implicit fields learning tasks such as SDF learning or NeRF. From extensive quantitative and qualitative comparisons, TaylorGrid achieves a balance between the linear grid and neural voxels, showing its superiority in fast and high-quality implicit field learning.