Target-Independent Active Learning via Distribution-Splitting
Paper and Code
Sep 28, 2018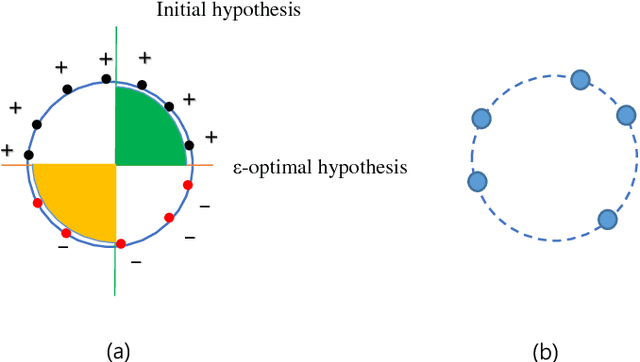
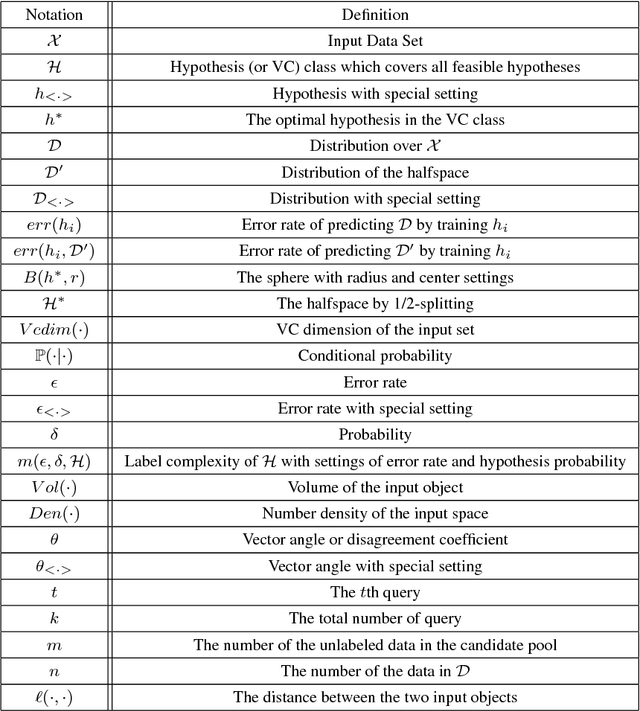
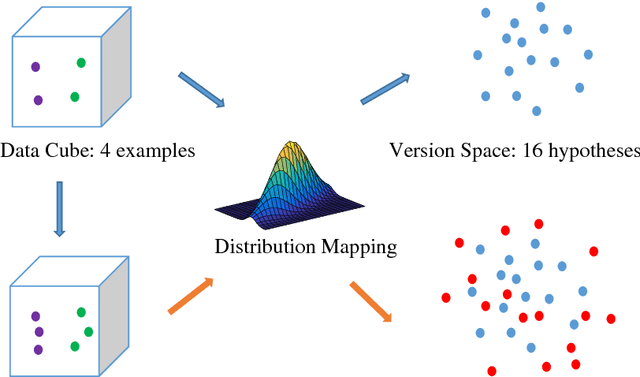
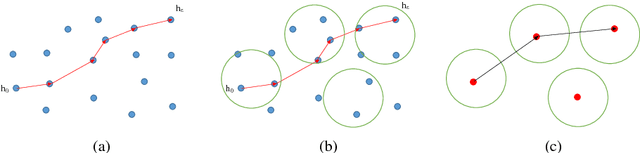
To reduce the label complexity in Agnostic Active Learning (A^2 algorithm), volume-splitting splits the hypothesis edges to reduce the Vapnik-Chervonenkis (VC) dimension in version space. However, the effectiveness of volume-splitting critically depends on the initial hypothesis and this problem is also known as target-dependent label complexity gap. This paper attempts to minimize this gap by introducing a novel notion of number density which provides a more natural and direct way to describe the hypothesis distribution than volume. By discovering the connections between hypothesis and input distribution, we map the volume of version space into the number density and propose a target-independent distribution-splitting strategy with the following advantages: 1) provide theoretical guarantees on reducing label complexity and error rate as volume-splitting; 2) break the curse of initial hypothesis; 3) provide model guidance for a target-independent AL algorithm in real AL tasks. With these guarantees, for AL application, we then split the input distribution into more near-optimal spheres and develop an application algorithm called Distribution-based A^2 (DA^2). Experiments further verify the effectiveness of the halving and querying abilities of DA^2. Contributions of this paper are as follows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge