Tackling System and Statistical Heterogeneity for Federated Learning with Adaptive Client Sampling

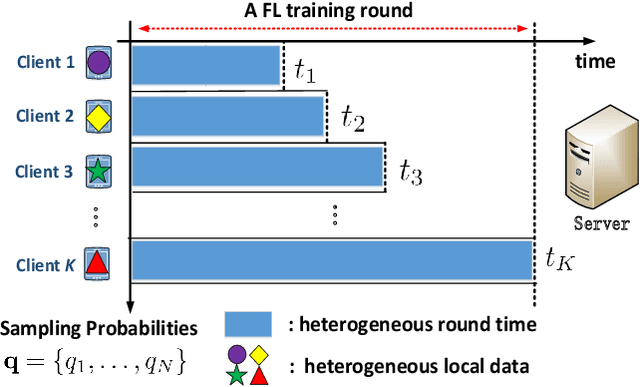
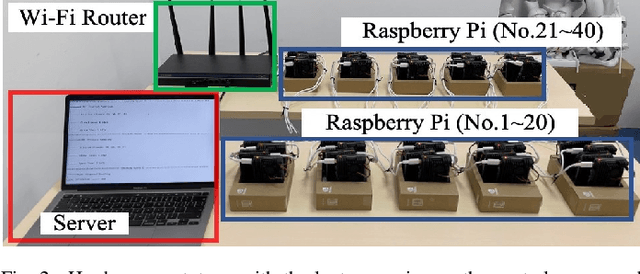
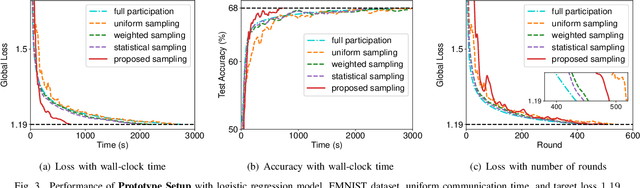
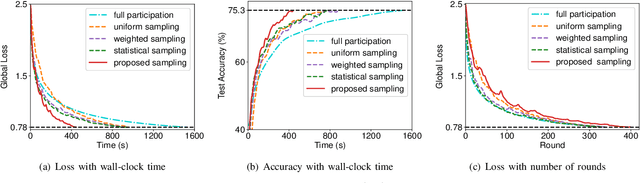
Federated learning (FL) algorithms usually sample a fraction of clients in each round (partial participation) when the number of participants is large and the server's communication bandwidth is limited. Recent works on the convergence analysis of FL have focused on unbiased client sampling, e.g., sampling uniformly at random, which suffers from slow wall-clock time for convergence due to high degrees of system heterogeneity and statistical heterogeneity. This paper aims to design an adaptive client sampling algorithm that tackles both system and statistical heterogeneity to minimize the wall-clock convergence time. We obtain a new tractable convergence bound for FL algorithms with arbitrary client sampling probabilities. Based on the bound, we analytically establish the relationship between the total learning time and sampling probabilities, which results in a non-convex optimization problem for training time minimization. We design an efficient algorithm for learning the unknown parameters in the convergence bound and develop a low-complexity algorithm to approximately solve the non-convex problem. Experimental results from both hardware prototype and simulation demonstrate that our proposed sampling scheme significantly reduces the convergence time compared to several baseline sampling schemes. Notably, our scheme in hardware prototype spends 73% less time than the uniform sampling baseline for reaching the same target loss.