Sum of Us: Strategyproof Selection from the Selectors
Paper and Code
Oct 25, 2009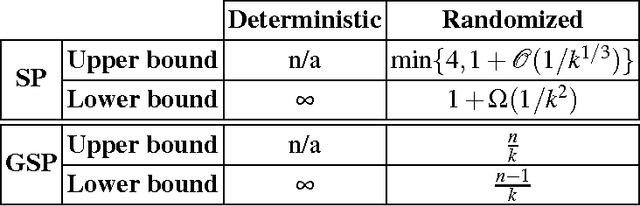
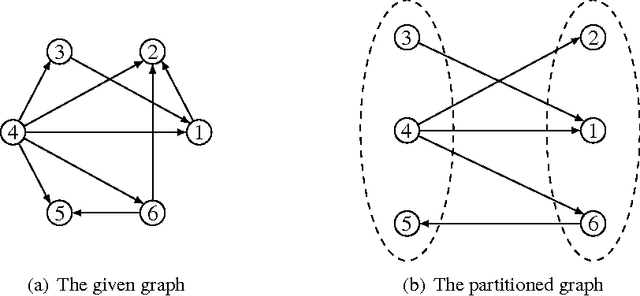
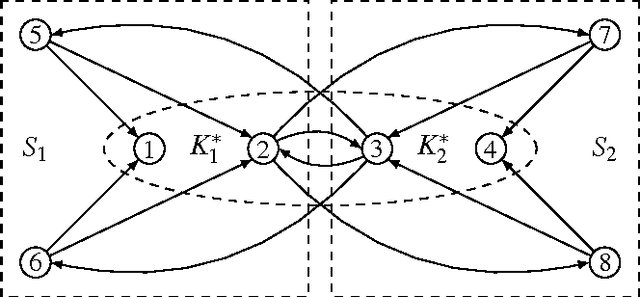

We consider directed graphs over a set of n agents, where an edge (i,j) is taken to mean that agent i supports or trusts agent j. Given such a graph and an integer k\leq n, we wish to select a subset of k agents that maximizes the sum of indegrees, i.e., a subset of k most popular or most trusted agents. At the same time we assume that each individual agent is only interested in being selected, and may misreport its outgoing edges to this end. This problem formulation captures realistic scenarios where agents choose among themselves, which can be found in the context of Internet search, social networks like Twitter, or reputation systems like Epinions. Our goal is to design mechanisms without payments that map each graph to a k-subset of agents to be selected and satisfy the following two constraints: strategyproofness, i.e., agents cannot benefit from misreporting their outgoing edges, and approximate optimality, i.e., the sum of indegrees of the selected subset of agents is always close to optimal. Our first main result is a surprising impossibility: for k \in {1,...,n-1}, no deterministic strategyproof mechanism can provide a finite approximation ratio. Our second main result is a randomized strategyproof mechanism with an approximation ratio that is bounded from above by four for any value of k, and approaches one as k grows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge