Streaming Robust Submodular Maximization: A Partitioned Thresholding Approach
Paper and Code
Nov 07, 2017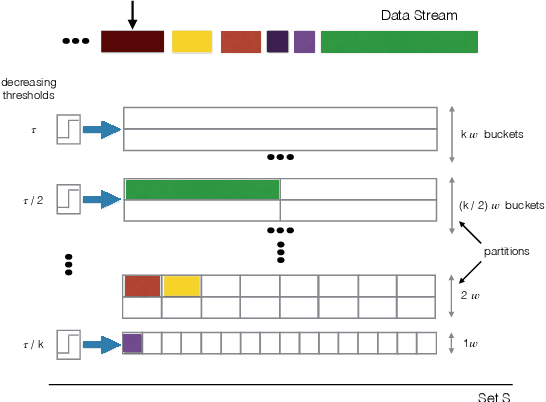
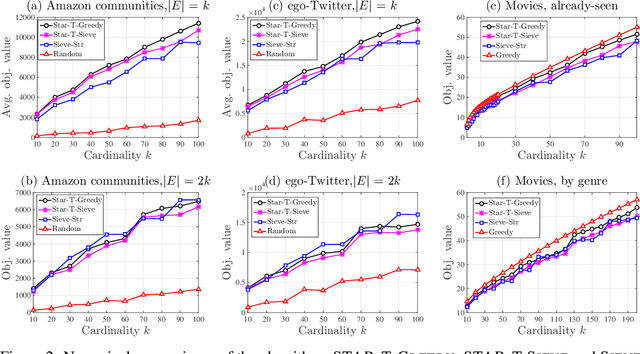
We study the classical problem of maximizing a monotone submodular function subject to a cardinality constraint k, with two additional twists: (i) elements arrive in a streaming fashion, and (ii) m items from the algorithm's memory are removed after the stream is finished. We develop a robust submodular algorithm STAR-T. It is based on a novel partitioning structure and an exponentially decreasing thresholding rule. STAR-T makes one pass over the data and retains a short but robust summary. We show that after the removal of any m elements from the obtained summary, a simple greedy algorithm STAR-T-GREEDY that runs on the remaining elements achieves a constant-factor approximation guarantee. In two different data summarization tasks, we demonstrate that it matches or outperforms existing greedy and streaming methods, even if they are allowed the benefit of knowing the removed subset in advance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge