Straggler-Resilient Distributed Machine Learning with Dynamic Backup Workers
Paper and Code
Feb 11, 2021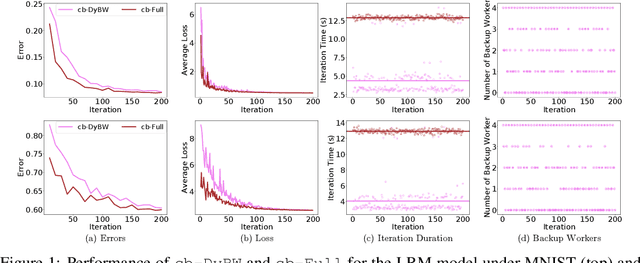

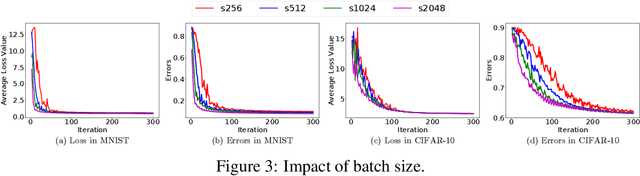
With the increasing demand for large-scale training of machine learning models, consensus-based distributed optimization methods have recently been advocated as alternatives to the popular parameter server framework. In this paradigm, each worker maintains a local estimate of the optimal parameter vector, and iteratively updates it by waiting and averaging all estimates obtained from its neighbors, and then corrects it on the basis of its local dataset. However, the synchronization phase can be time consuming due to the need to wait for \textit{stragglers}, i.e., slower workers. An efficient way to mitigate this effect is to let each worker wait only for updates from the fastest neighbors before updating its local parameter. The remaining neighbors are called \textit{backup workers.} To minimize the globally training time over the network, we propose a fully distributed algorithm to dynamically determine the number of backup workers for each worker. We show that our algorithm achieves a linear speedup for convergence (i.e., convergence performance increases linearly with respect to the number of workers). We conduct extensive experiments on MNIST and CIFAR-10 to verify our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge