Stochastic Shortest Path: Minimax, Parameter-Free and Towards Horizon-Free Regret
Paper and Code
Apr 22, 2021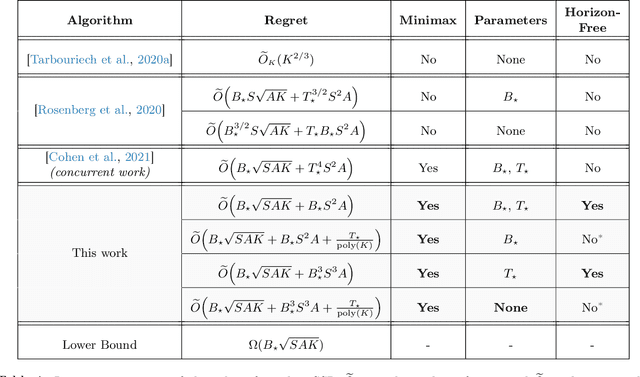
We study the problem of learning in the stochastic shortest path (SSP) setting, where an agent seeks to minimize the expected cost accumulated before reaching a goal state. We design a novel model-based algorithm EB-SSP that carefully skews the empirical transitions and perturbs the empirical costs with an exploration bonus to guarantee both optimism and convergence of the associated value iteration scheme. We prove that EB-SSP achieves the minimax regret rate $\widetilde{O}(B_{\star} \sqrt{S A K})$, where $K$ is the number of episodes, $S$ is the number of states, $A$ is the number of actions and $B_{\star}$ bounds the expected cumulative cost of the optimal policy from any state, thus closing the gap with the lower bound. Interestingly, EB-SSP obtains this result while being parameter-free, i.e., it does not require any prior knowledge of $B_{\star}$, nor of $T_{\star}$ which bounds the expected time-to-goal of the optimal policy from any state. Furthermore, we illustrate various cases (e.g., positive costs, or general costs when an order-accurate estimate of $T_{\star}$ is available) where the regret only contains a logarithmic dependence on $T_{\star}$, thus yielding the first horizon-free regret bound beyond the finite-horizon MDP setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge