Stein Variational Policy Gradient
Paper and Code
Apr 07, 2017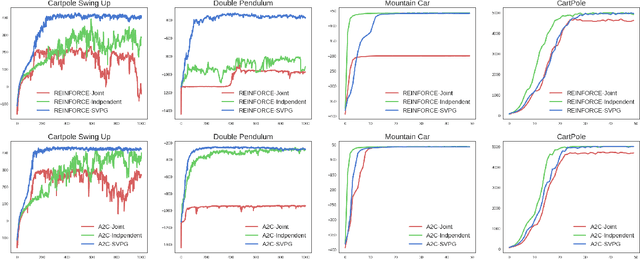
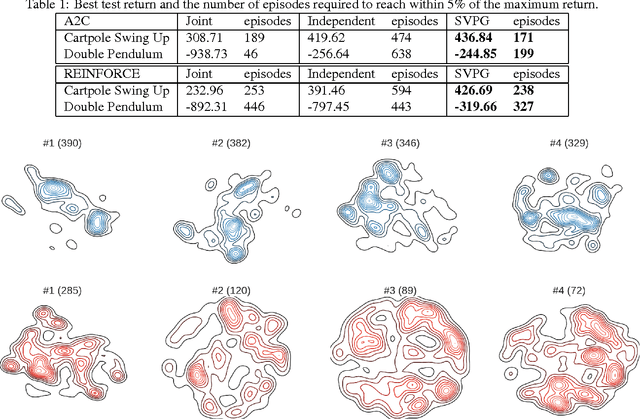
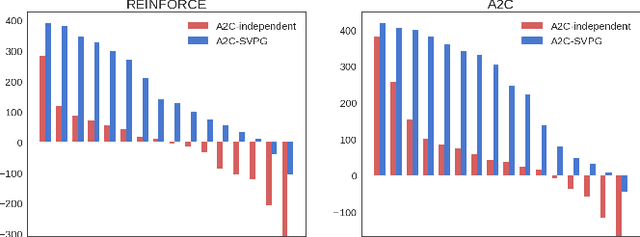
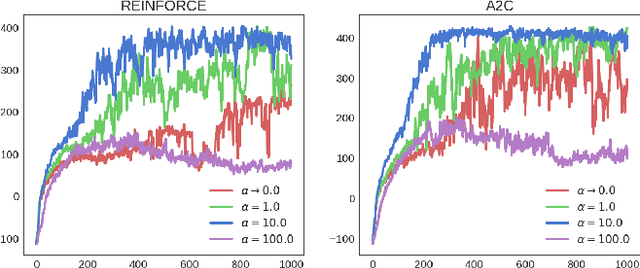
Policy gradient methods have been successfully applied to many complex reinforcement learning problems. However, policy gradient methods suffer from high variance, slow convergence, and inefficient exploration. In this work, we introduce a maximum entropy policy optimization framework which explicitly encourages parameter exploration, and show that this framework can be reduced to a Bayesian inference problem. We then propose a novel Stein variational policy gradient method (SVPG) which combines existing policy gradient methods and a repulsive functional to generate a set of diverse but well-behaved policies. SVPG is robust to initialization and can easily be implemented in a parallel manner. On continuous control problems, we find that implementing SVPG on top of REINFORCE and advantage actor-critic algorithms improves both average return and data efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge