Statistical Hypothesis Testing for Class-Conditional Label Noise

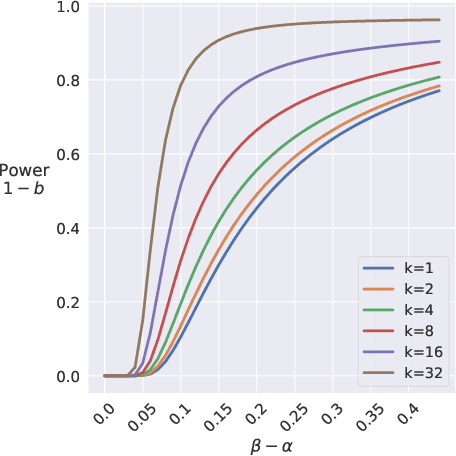
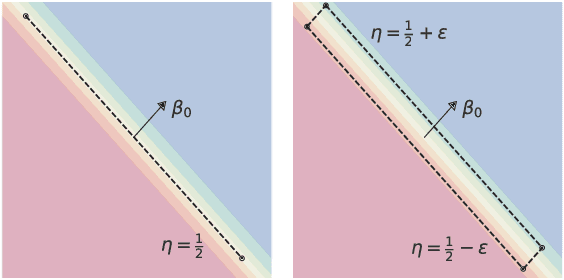
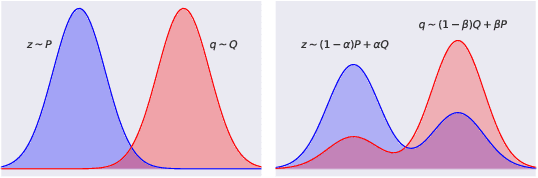
In this work we aim to provide machine learning practitioners with tools to answer the question: is there class-conditional flipping noise in my labels? In particular, we present hypothesis tests to reliably check whether a given dataset of instance-label pairs has been corrupted with class-conditional label noise. While previous works explore the direct estimation of the noise rates, this is known to be hard in practice and does not offer a real understanding of how trustworthy the estimates are. These methods typically require anchor points - examples whose true posterior is either 0 or 1. Differently, in this paper we assume we have access to a set of anchor points whose true posterior is approximately 1/2. The proposed hypothesis tests are built upon the asymptotic properties of Maximum Likelihood Estimators for Logistic Regression models and accurately distinguish the presence of class-conditional noise from uniform noise. We establish the main properties of the tests, including a theoretical and empirical analysis of the dependence of the power on the test on the training sample size, the number of anchor points, the difference of the noise rates and the use of realistic relaxed anchors.