sqSGD: Locally Private and Communication Efficient Federated Learning
Paper and Code
Jun 22, 2022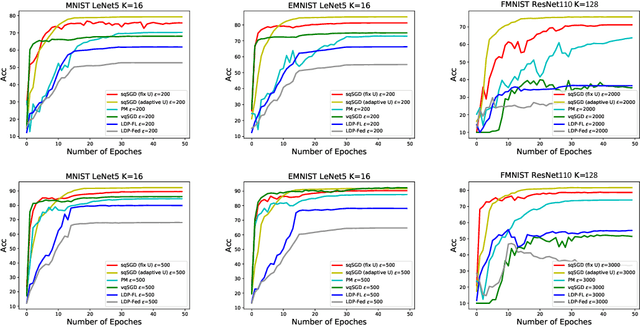
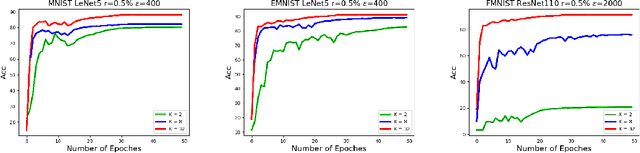
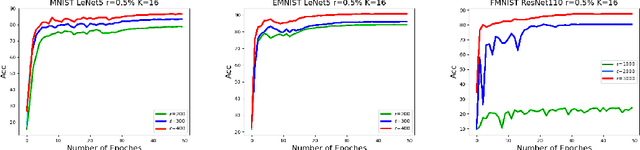
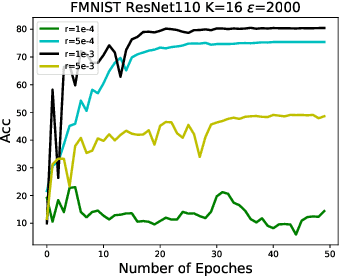
Federated learning (FL) is a technique that trains machine learning models from decentralized data sources. We study FL under local notions of privacy constraints, which provides strong protection against sensitive data disclosures via obfuscating the data before leaving the client. We identify two major concerns in designing practical privacy-preserving FL algorithms: communication efficiency and high-dimensional compatibility. We then develop a gradient-based learning algorithm called \emph{sqSGD} (selective quantized stochastic gradient descent) that addresses both concerns. The proposed algorithm is based on a novel privacy-preserving quantization scheme that uses a constant number of bits per dimension per client. Then we improve the base algorithm in three ways: first, we apply a gradient subsampling strategy that simultaneously offers better training performance and smaller communication costs under a fixed privacy budget. Secondly, we utilize randomized rotation as a preprocessing step to reduce quantization error. Thirdly, an adaptive gradient norm upper bound shrinkage strategy is adopted to improve accuracy and stabilize training. Finally, the practicality of the proposed framework is demonstrated on benchmark datasets. Experiment results show that sqSGD successfully learns large models like LeNet and ResNet with local privacy constraints. In addition, with fixed privacy and communication level, the performance of sqSGD significantly dominates that of various baseline algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge