SPEED: Experimental Design for Policy Evaluation in Linear Heteroscedastic Bandits

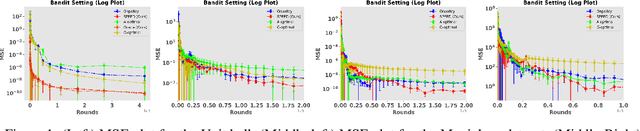
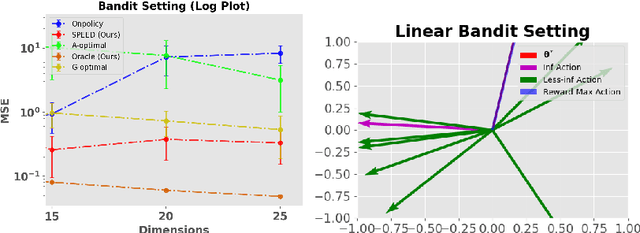
In this paper, we study the problem of optimal data collection for policy evaluation in linear bandits. In policy evaluation, we are given a target policy and asked to estimate the expected cumulative reward it will obtain when executed in an environment formalized as a multi-armed bandit. In this paper, we focus on linear bandit setting with heteroscedastic reward noise. This is the first work that focuses on such an optimal data collection strategy for policy evaluation involving heteroscedastic reward noise in the linear bandit setting. We first formulate an optimal design for weighted least squares estimates in the heteroscedastic linear bandit setting that reduces the MSE of the target policy. We term this as policy-weighted least square estimation and use this formulation to derive the optimal behavior policy for data collection. We then propose a novel algorithm SPEED (Structured Policy Evaluation Experimental Design) that tracks the optimal behavior policy and derive its regret with respect to the optimal behavior policy. Finally, we empirically validate that SPEED leads to policy evaluation with mean squared error comparable to the oracle strategy and significantly lower than simply running the target policy.