Sparse Spectrum Gaussian Process for Bayesian Optimisation

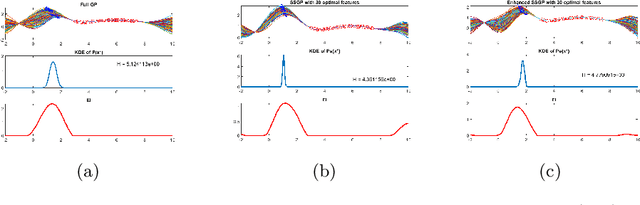
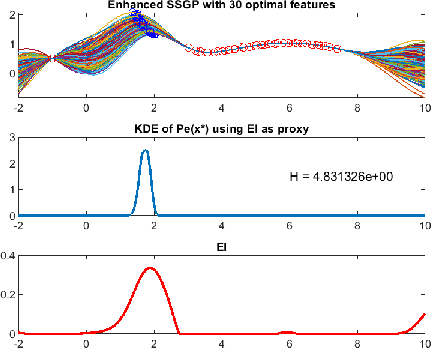
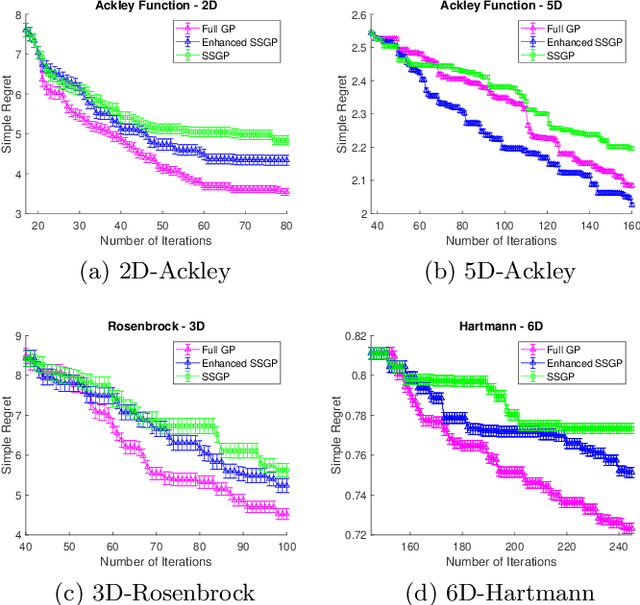
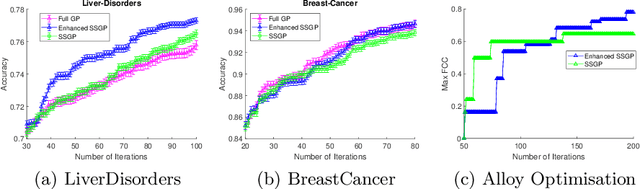
We propose a novel sparse spectrum approximation of Gaussian process (GP) tailored for Bayesian optimisation. Whilst the current sparse spectrum methods provide good approximations for regression problems, it is observed that this particular form of sparse approximations generates an overconfident GP, i.e. it predicts less variance than the original GP. Since the balance between predictive mean and the predictive variance is a key determinant in the success of Bayesian optimisation, the current sparse spectrum methods are less suitable. We derive a regularised marginal likelihood for finding the optimal frequencies in optimisation problems. The regulariser trades the accuracy in the model fitting with the targeted increase in the variance of the resultant GP. We first consider the entropy of the distribution over the maxima as the regulariser that needs to be maximised. Later we show that the Expected Improvement acquisition function can also be used as a proxy for that, thus making the optimisation less computationally expensive. Experiments show an increase in the Bayesian optimisation convergence rate over the vanilla sparse spectrum method.