SOM-Net: Unrolling the Subspace-based Optimization for Solving Full-wave Inverse Scattering Problems
Paper and Code
Sep 08, 2022
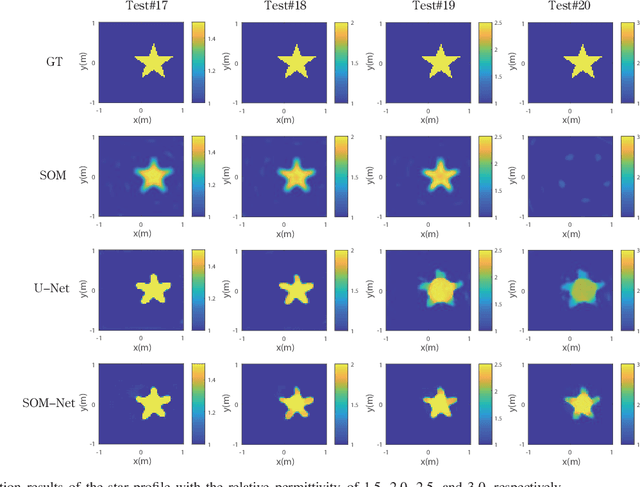
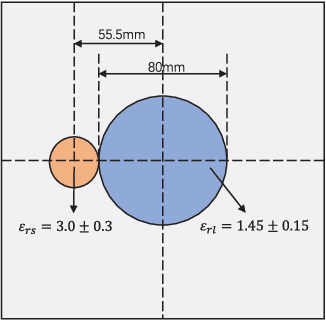

In this paper, an unrolling algorithm of the iterative subspace-based optimization method (SOM) is proposed for solving full-wave inverse scattering problems (ISPs). The unrolling network, named SOM-Net, inherently embeds the Lippmann- Schwinger physical model into the design of network structures. The SOM-Net takes the deterministic induced current and the raw permittivity image obtained from back-propagation (BP) as the input. It then updates the induced current and the permittivity successively in sub-network blocks of the SOM- Net by imitating iterations of the SOM. The final output of the SOM-Net is the full predicted induced current, from which the scattered field and the permittivity image can also be deduced analytically. The parameters of the SOM-Net are optimized in a supervised manner with the total loss to simultaneously ensure the consistency of the induced current, the scattered field, and the permittivity in the governing equations. Numerical tests on both synthetic and experimental data verify the superior performance of the proposed SOM-Net over typical ones. The results on challenging examples like scatterers with tough profiles or high permittivity demonstrate the good generalization ability of the SOM-Net. With the use of deep unrolling technology, this work builds a bridge between traditional iterative methods and deep learning methods for solving ISPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge