Smoothing proximal gradient method for general structured sparse regression
Paper and Code
Jun 29, 2012
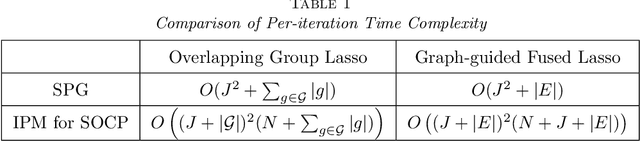
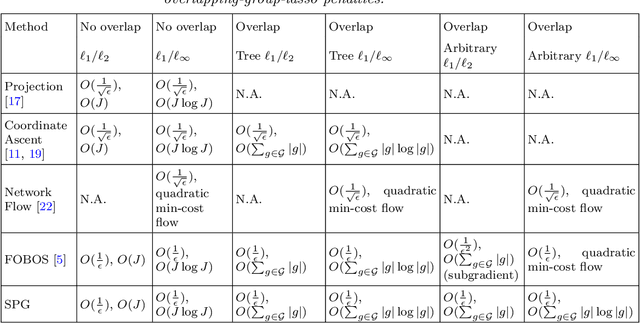
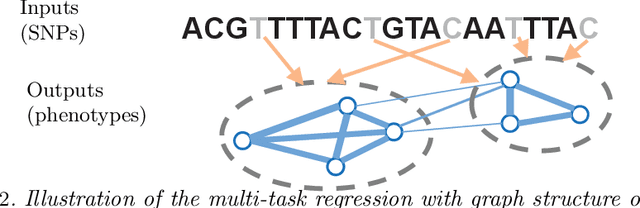
We study the problem of estimating high-dimensional regression models regularized by a structured sparsity-inducing penalty that encodes prior structural information on either the input or output variables. We consider two widely adopted types of penalties of this kind as motivating examples: (1) the general overlapping-group-lasso penalty, generalized from the group-lasso penalty; and (2) the graph-guided-fused-lasso penalty, generalized from the fused-lasso penalty. For both types of penalties, due to their nonseparability and nonsmoothness, developing an efficient optimization method remains a challenging problem. In this paper we propose a general optimization approach, the smoothing proximal gradient (SPG) method, which can solve structured sparse regression problems with any smooth convex loss under a wide spectrum of structured sparsity-inducing penalties. Our approach combines a smoothing technique with an effective proximal gradient method. It achieves a convergence rate significantly faster than the standard first-order methods, subgradient methods, and is much more scalable than the most widely used interior-point methods. The efficiency and scalability of our method are demonstrated on both simulation experiments and real genetic data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge