SmoothI: Smooth Rank Indicators for Differentiable IR Metrics
Paper and Code
May 03, 2021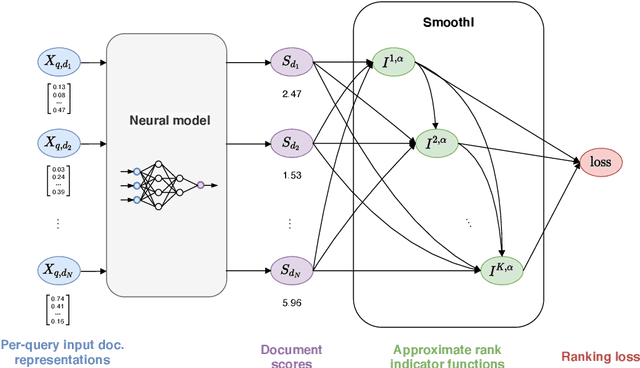
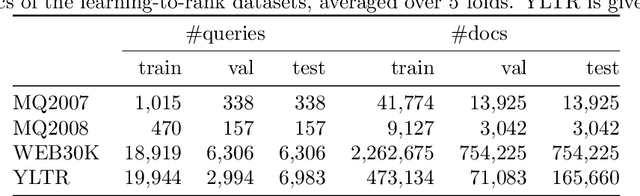
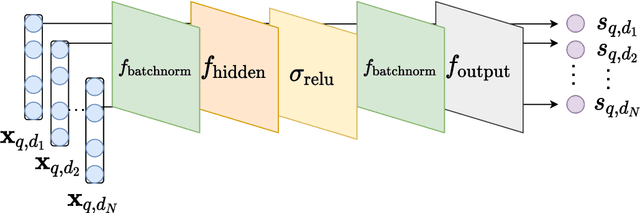
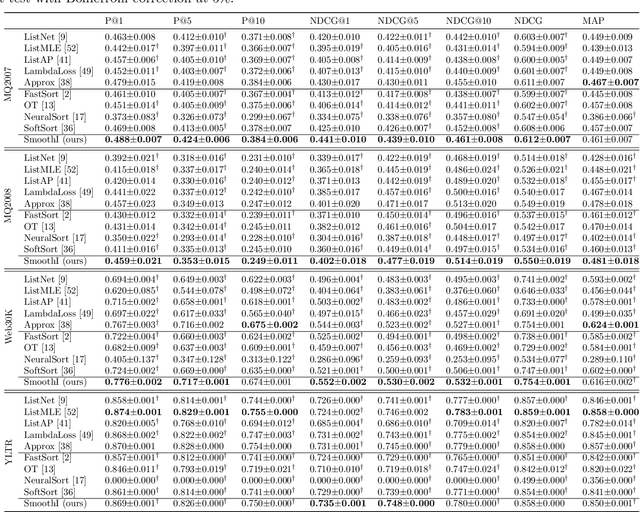
Information retrieval (IR) systems traditionally aim to maximize metrics built on rankings, such as precision or NDCG. However, the non-differentiability of the ranking operation prevents direct optimization of such metrics in state-of-the-art neural IR models, which rely entirely on the ability to compute meaningful gradients. To address this shortcoming, we propose SmoothI, a smooth approximation of rank indicators that serves as a basic building block to devise differentiable approximations of IR metrics. We further provide theoretical guarantees on SmoothI and derived approximations, showing in particular that the approximation errors decrease exponentially with an inverse temperature-like hyperparameter that controls the quality of the approximations. Extensive experiments conducted on four standard learning-to-rank datasets validate the efficacy of the listwise losses based on SmoothI, in comparison to previously proposed ones. Additional experiments with a vanilla BERT ranking model on a text-based IR task also confirm the benefits of our listwise approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge