SketchSampler: Sketch-based 3D Reconstruction via View-dependent Depth Sampling
Paper and Code
Aug 14, 2022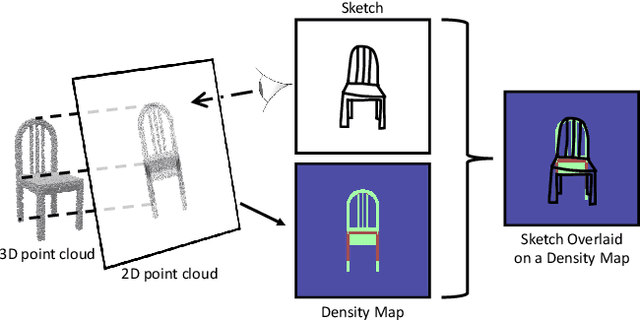
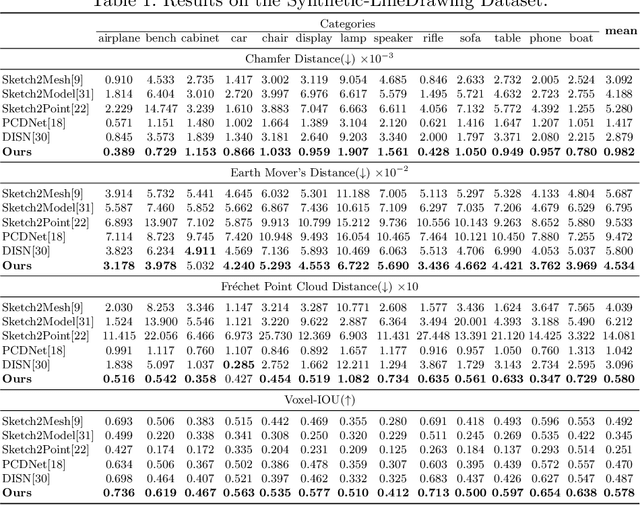
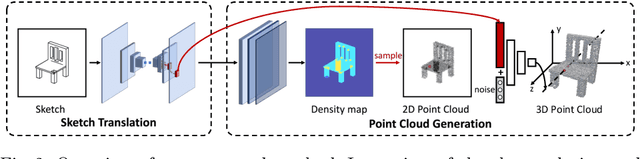
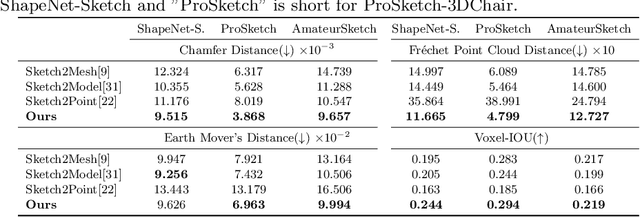
Reconstructing a 3D shape based on a single sketch image is challenging due to the large domain gap between a sparse, irregular sketch and a regular, dense 3D shape. Existing works try to employ the global feature extracted from sketch to directly predict the 3D coordinates, but they usually suffer from losing fine details that are not faithful to the input sketch. Through analyzing the 3D-to-2D projection process, we notice that the density map that characterizes the distribution of 2D point clouds (i.e., the probability of points projected at each location of the projection plane) can be used as a proxy to facilitate the reconstruction process. To this end, we first translate a sketch via an image translation network to a more informative 2D representation that can be used to generate a density map. Next, a 3D point cloud is reconstructed via a two-stage probabilistic sampling process: first recovering the 2D points (i.e., the x and y coordinates) by sampling the density map; and then predicting the depth (i.e., the z coordinate) by sampling the depth values at the ray determined by each 2D point. Extensive experiments are conducted, and both quantitative and qualitative results show that our proposed approach significantly outperforms other baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge