Self-Paced Learning: an Implicit Regularization Perspective
Paper and Code
Sep 18, 2016
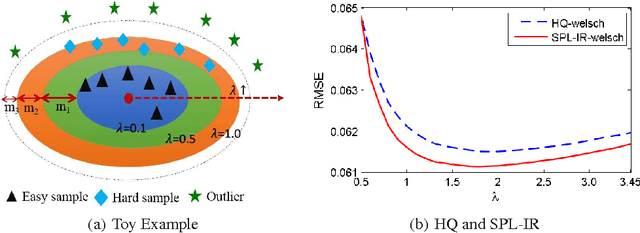
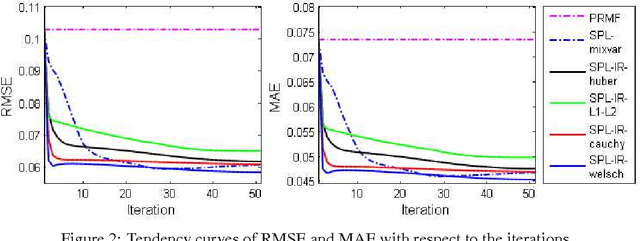

Self-paced learning (SPL) mimics the cognitive mechanism of humans and animals that gradually learns from easy to hard samples. One key issue in SPL is to obtain better weighting strategy that is determined by minimizer function. Existing methods usually pursue this by artificially designing the explicit form of SPL regularizer. In this paper, we focus on the minimizer function, and study a group of new regularizer, named self-paced implicit regularizer that is deduced from robust loss function. Based on the convex conjugacy theory, the minimizer function for self-paced implicit regularizer can be directly learned from the latent loss function, while the analytic form of the regularizer can be even known. A general framework (named SPL-IR) for SPL is developed accordingly. We demonstrate that the learning procedure of SPL-IR is associated with latent robust loss functions, thus can provide some theoretical inspirations for its working mechanism. We further analyze the relation between SPL-IR and half-quadratic optimization. Finally, we implement SPL-IR to both supervised and unsupervised tasks, and experimental results corroborate our ideas and demonstrate the correctness and effectiveness of implicit regularizers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge