Seeing the Forest from the Trees in Two Looks: Matrix Sketching by Cascaded Bilateral Sampling
Paper and Code
Jul 27, 2016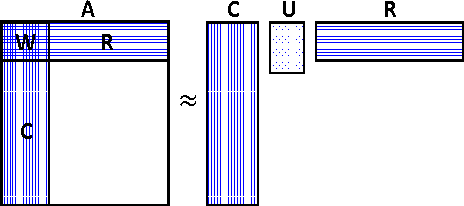

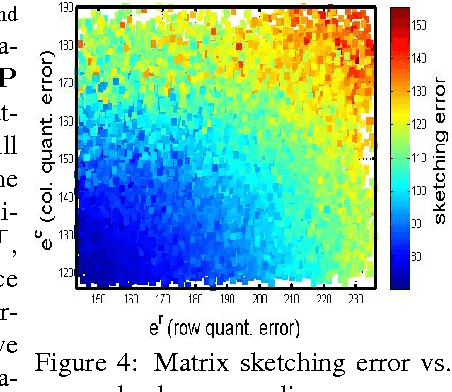
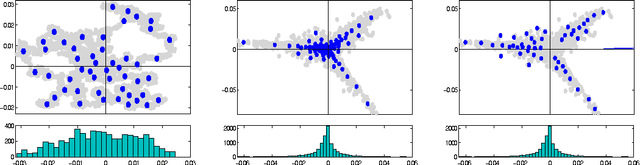
Matrix sketching is aimed at finding close approximations of a matrix by factors of much smaller dimensions, which has important applications in optimization and machine learning. Given a matrix A of size m by n, state-of-the-art randomized algorithms take O(m * n) time and space to obtain its low-rank decomposition. Although quite useful, the need to store or manipulate the entire matrix makes it a computational bottleneck for truly large and dense inputs. Can we sketch an m-by-n matrix in O(m + n) cost by accessing only a small fraction of its rows and columns, without knowing anything about the remaining data? In this paper, we propose the cascaded bilateral sampling (CABS) framework to solve this problem. We start from demonstrating how the approximation quality of bilateral matrix sketching depends on the encoding powers of sampling. In particular, the sampled rows and columns should correspond to the code-vectors in the ground truth decompositions. Motivated by this analysis, we propose to first generate a pilot-sketch using simple random sampling, and then pursue more advanced, "follow-up" sampling on the pilot-sketch factors seeking maximal encoding powers. In this cascading process, the rise of approximation quality is shown to be lower-bounded by the improvement of encoding powers in the follow-up sampling step, thus theoretically guarantees the algorithmic boosting property. Computationally, our framework only takes linear time and space, and at the same time its performance rivals the quality of state-of-the-art algorithms consuming a quadratic amount of resources. Empirical evaluations on benchmark data fully demonstrate the potential of our methods in large scale matrix sketching and related areas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge