Scaling Laws for Discriminative Speech Recognition Rescoring Models
Paper and Code
Jun 27, 2023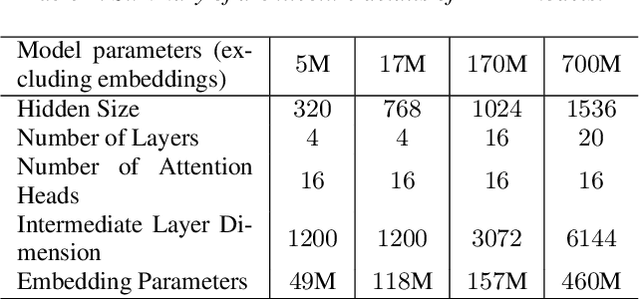
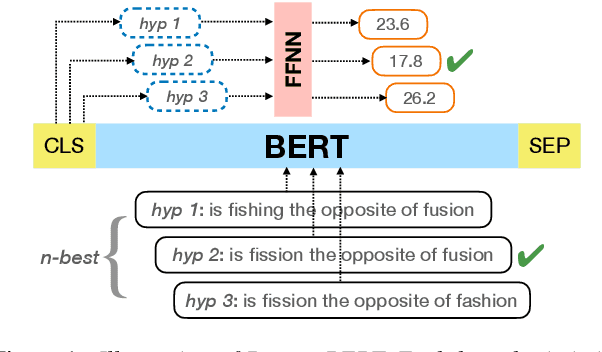
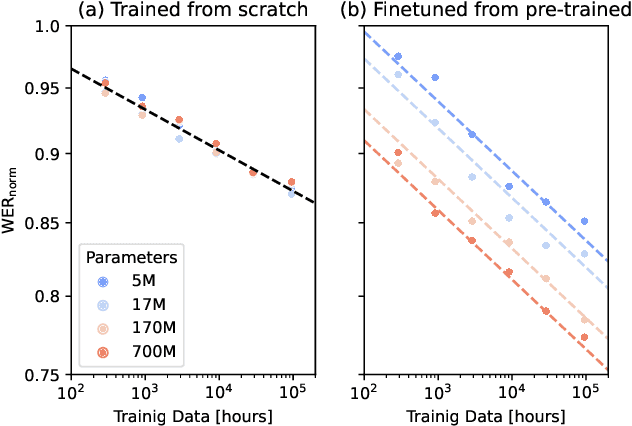
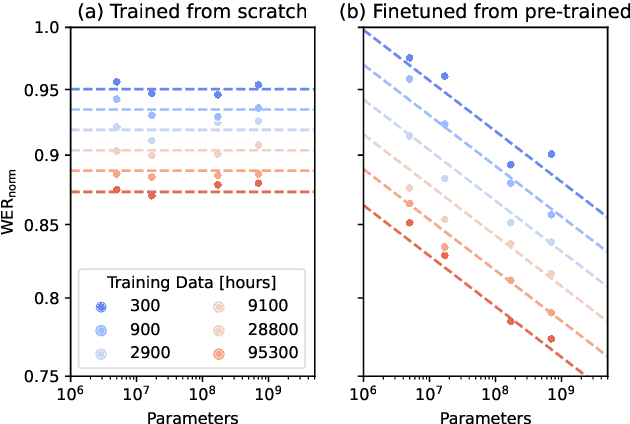
Recent studies have found that model performance has a smooth power-law relationship, or scaling laws, with training data and model size, for a wide range of problems. These scaling laws allow one to choose nearly optimal data and model sizes. We study whether this scaling property is also applicable to second-pass rescoring, which is an important component of speech recognition systems. We focus on RescoreBERT as the rescoring model, which uses a pre-trained Transformer-based architecture fined tuned with an ASR discriminative loss. Using such a rescoring model, we show that the word error rate (WER) follows a scaling law for over two orders of magnitude as training data and model size increase. In addition, it is found that a pre-trained model would require less data than a randomly initialized model of the same size, representing effective data transferred from pre-training step. This effective data transferred is found to also follow a scaling law with the data and model size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge