Scalable photonic reinforcement learning by time-division multiplexing of laser chaos
Paper and Code
Mar 26, 2018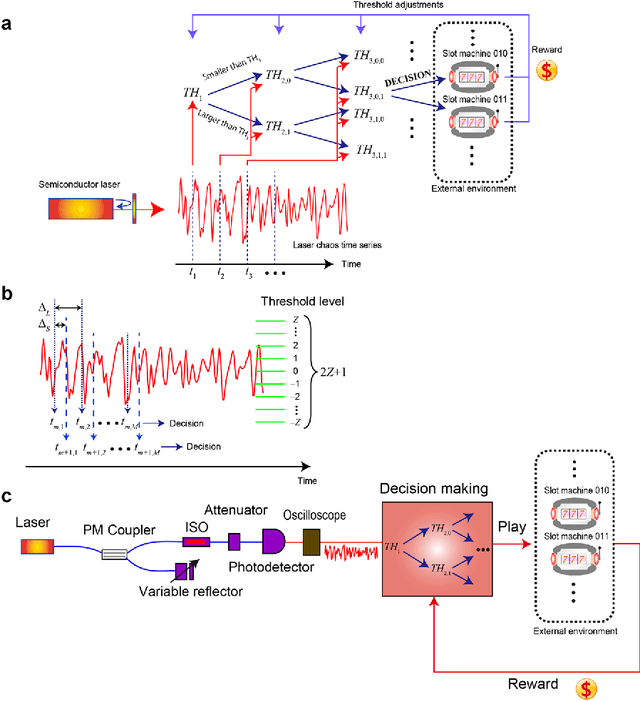

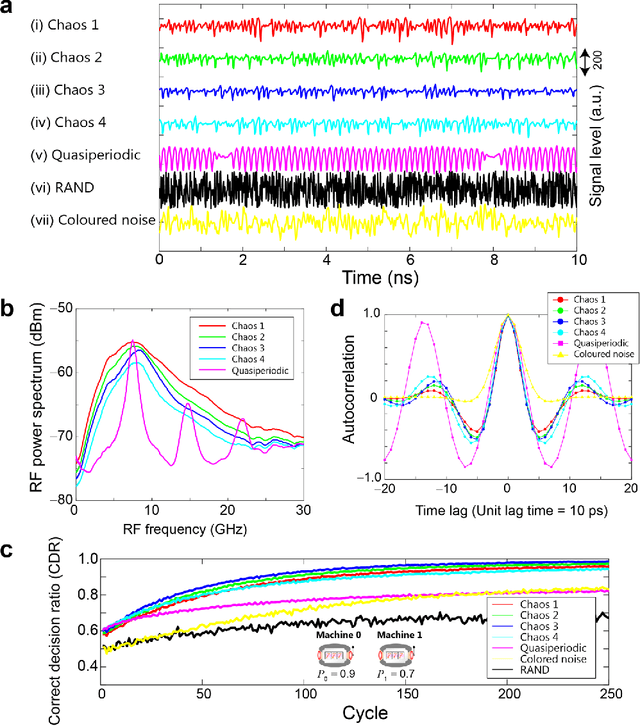
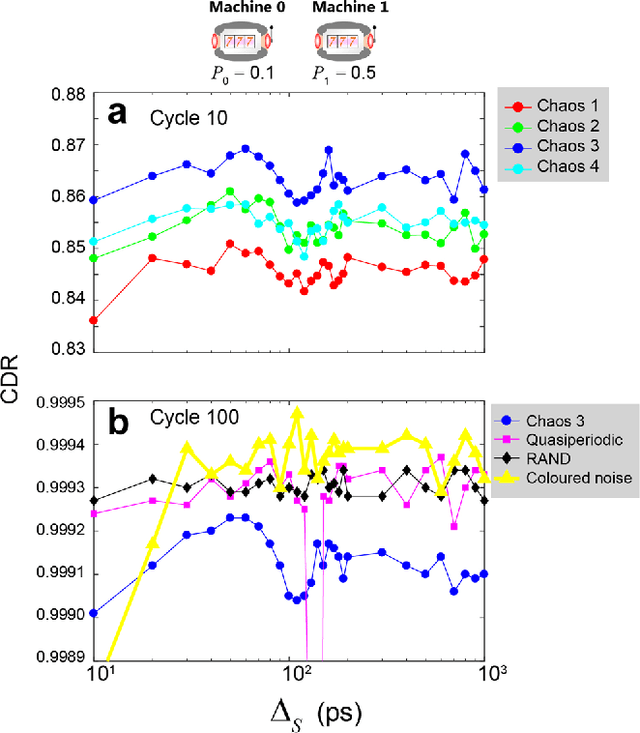
Reinforcement learning involves decision making in dynamic and uncertain environments and constitutes a crucial element of artificial intelligence. In our previous work, we experimentally demonstrated that the ultrafast chaotic oscillatory dynamics of lasers can be used to solve the two-armed bandit problem efficiently, which requires decision making concerning a class of difficult trade-offs called the exploration-exploitation dilemma. However, only two selections were employed in that research; thus, the scalability of the laser-chaos-based reinforcement learning should be clarified. In this study, we demonstrated a scalable, pipelined principle of resolving the multi-armed bandit problem by introducing time-division multiplexing of chaotically oscillated ultrafast time-series. The experimental demonstrations in which bandit problems with up to 64 arms were successfully solved are presented in this report. Detailed analyses are also provided that include performance comparisons among laser chaos signals generated in different physical conditions, which coincide with the diffusivity inherent in the time series. This study paves the way for ultrafast reinforcement learning by taking advantage of the ultrahigh bandwidths of light wave and practical enabling technologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge