Scalable Bayesian Deep Learning with Kernel Seed Networks
Paper and Code
Apr 19, 2021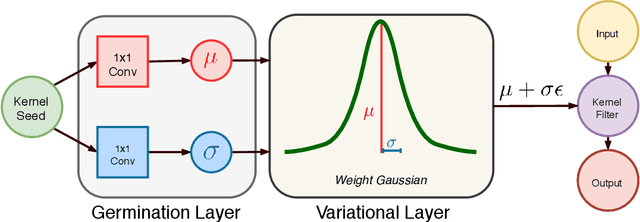
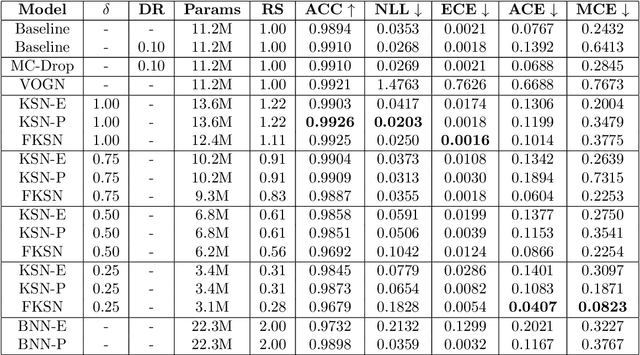
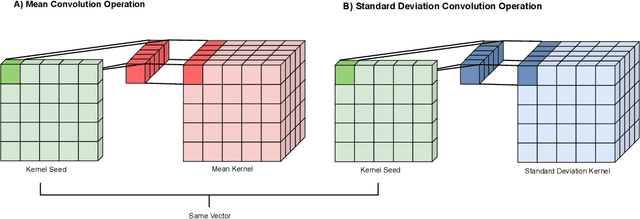
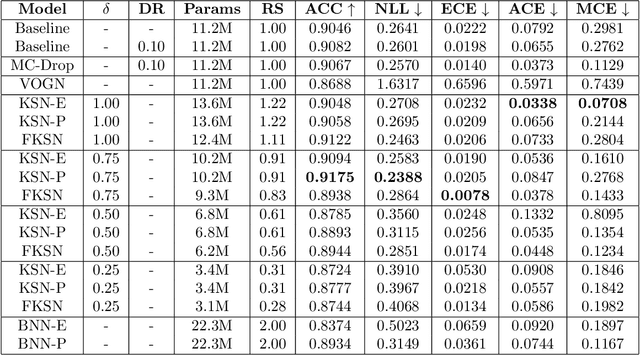
This paper addresses the scalability problem of Bayesian deep neural networks. The performance of deep neural networks is undermined by the fact that these algorithms have poorly calibrated measures of uncertainty. This restricts their application in high risk domains such as computer aided diagnosis and autonomous vehicle navigation. Bayesian Deep Learning (BDL) offers a promising method for representing uncertainty in neural network. However, BDL requires a separate set of parameters to store the mean and standard deviation of model weights to learn a distribution. This results in a prohibitive 2-fold increase in the number of model parameters. To address this problem we present a method for performing BDL, namely Kernel Seed Networks (KSN), which does not require a 2-fold increase in the number of parameters. KSNs use 1x1 Convolution operations to learn a compressed latent space representation of the parameter distribution. In this paper we show how this allows KSNs to outperform conventional BDL methods while reducing the number of required parameters by up to a factor of 6.6.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge