Safeguarded Progress in Reinforcement Learning: Safe Bayesian Exploration for Control Policy Synthesis
Paper and Code
Dec 18, 2023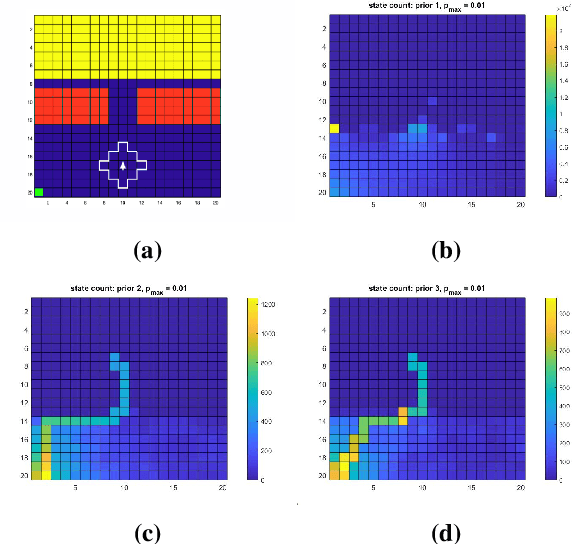
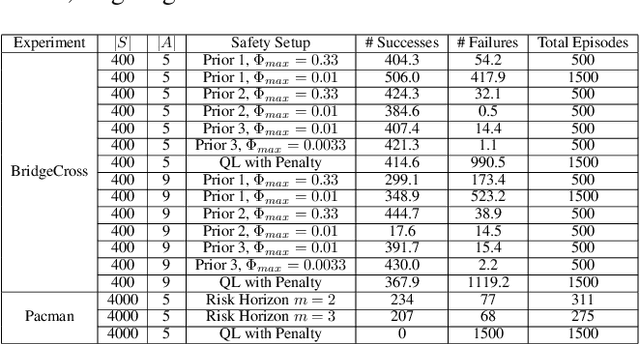
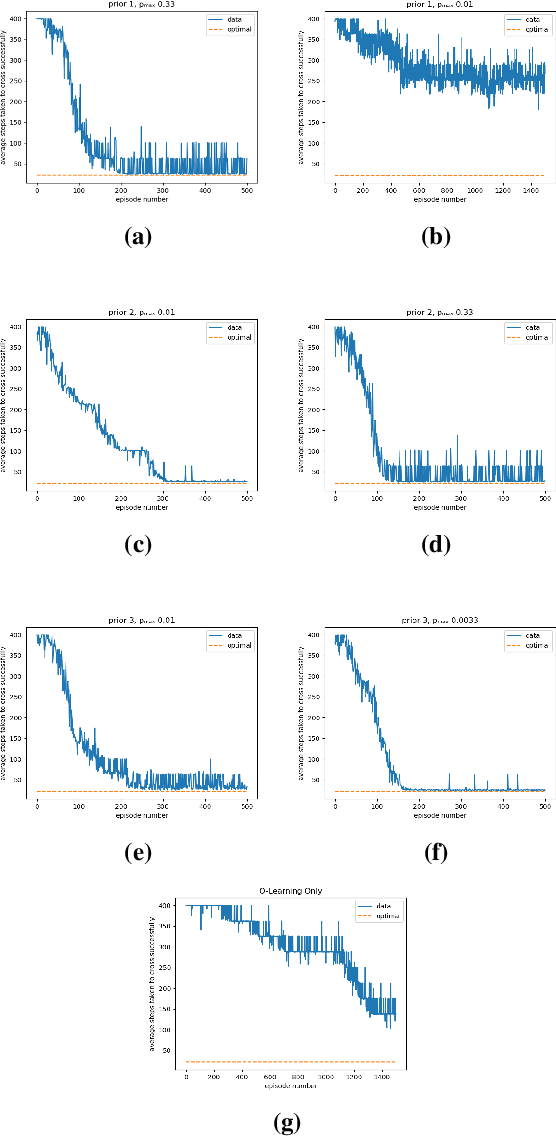
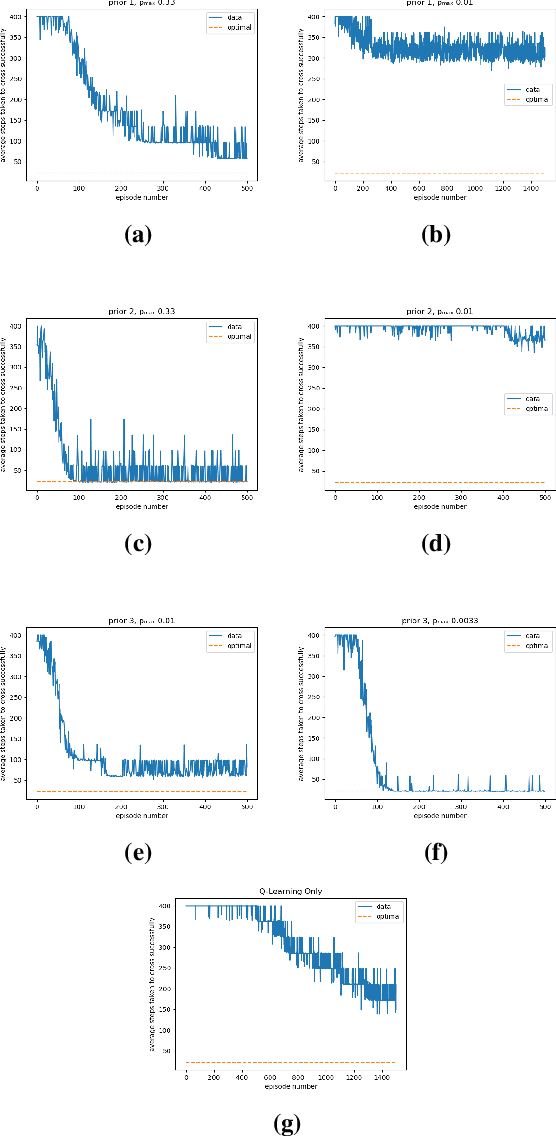
This paper addresses the problem of maintaining safety during training in Reinforcement Learning (RL), such that the safety constraint violations are bounded at any point during learning. In a variety of RL applications the safety of the agent is particularly important, e.g. autonomous platforms or robots that work in proximity of humans. As enforcing safety during training might severely limit the agent's exploration, we propose here a new architecture that handles the trade-off between efficient progress and safety during exploration. As the exploration progresses, we update via Bayesian inference Dirichlet-Categorical models of the transition probabilities of the Markov decision process that describes the environment dynamics. This paper proposes a way to approximate moments of belief about the risk associated to the action selection policy. We construct those approximations, and prove the convergence results. We propose a novel method for leveraging the expectation approximations to derive an approximate bound on the confidence that the risk is below a certain level. This approach can be easily interleaved with RL and we present experimental results to showcase the performance of the overall architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge