Run-Time Efficient RNN Compression for Inference on Edge Devices

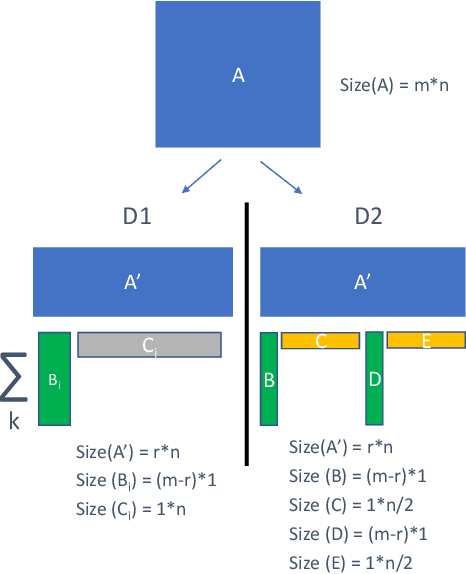
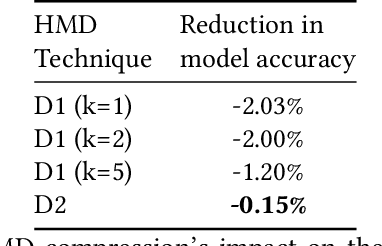
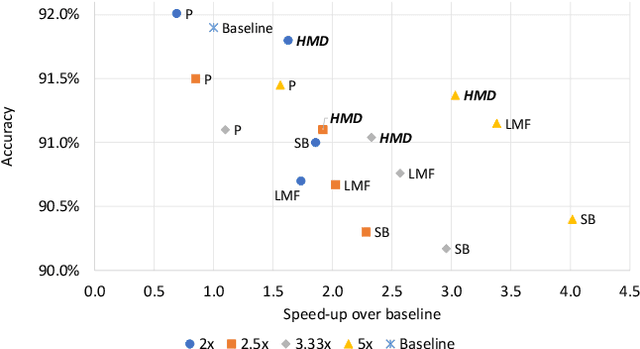
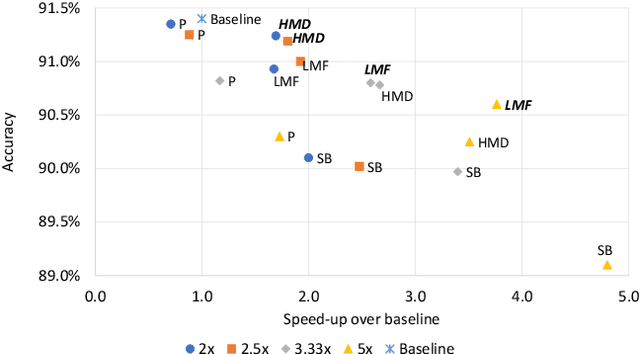
Recurrent neural networks can be large and compute-intensive, yet many applications that benefit from RNNs run on small devices with very limited compute and storage capabilities while still having run-time constraints. As a result, there is a need for compression techniques that can achieve significant compression without negatively impacting inference run-time and task accuracy. This paper explores a new compressed RNN cell implementation called Hybrid Matrix Decomposition (HMD) that achieves this dual objective. This scheme divides the weight matrix into two parts - an unconstrained upper half and a lower half composed of rank-1 blocks. This results in output features where the upper sub-vector has "richer" features while the lower-sub vector has "constrained" features". HMD can compress RNNs by a factor of 2-4x while having a faster run-time than pruning and retaining more model accuracy than matrix factorization. We evaluate this technique on 3 benchmarks.