ROML: A Robust Feature Correspondence Approach for Matching Objects in A Set of Images
Paper and Code
Mar 31, 2015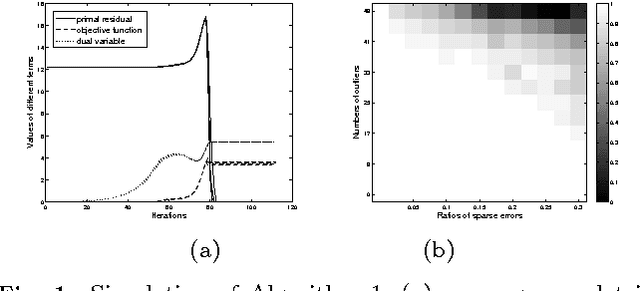
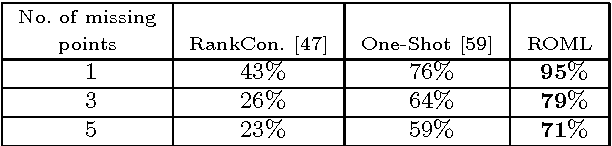


Feature-based object matching is a fundamental problem for many applications in computer vision, such as object recognition, 3D reconstruction, tracking, and motion segmentation. In this work, we consider simultaneously matching object instances in a set of images, where both inlier and outlier features are extracted. The task is to identify the inlier features and establish their consistent correspondences across the image set. This is a challenging combinatorial problem, and the problem complexity grows exponentially with the image number. To this end, we propose a novel framework, termed ROML, to address this problem. ROML optimizes simultaneously a partial permutation matrix (PPM) for each image, and feature correspondences are established by the obtained PPMs. Two of our key contributions are summarized as follows. (1) We formulate the problem as rank and sparsity minimization for PPM optimization, and treat simultaneous optimization of multiple PPMs as a regularized consensus problem in the context of distributed optimization. (2) We use the ADMM method to solve the thus formulated ROML problem, in which a subproblem associated with a single PPM optimization appears to be a difficult integer quadratic program (IQP). We prove that under wildly applicable conditions, this IQP is equivalent to a linear sum assignment problem (LSAP), which can be efficiently solved to an exact solution. Extensive experiments on rigid/non-rigid object matching, matching instances of a common object category, and common object localization show the efficacy of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge